如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=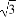AD,E为CD上一点,且CE=3DE.

(1)求证:AE⊥平面SBD.

(2)M,N分别为线段SB,CD上的点,是否存在M,N,使MN⊥CD且MN⊥SB,若存在,确定M,N的位置;若不存在,说明理由.

如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.

求证:(1)CM∥平面PAD.

(2)平面PAB⊥平面PAD.

设l,m,n为三条不同的直线,α,β为两个不同的平面,下列命题中正确的个数是(　　)

①若l⊥α,m∥β,α⊥β,则l⊥m;

②若m?α,n?α,l⊥m,l⊥n,则l⊥α;

③若l∥m,m∥n,l⊥α,则n⊥α;

④若l∥m,m⊥α,n⊥β,α∥β,则l∥n.

(A)1 (B)2 (C)3 (D)4

对于直线m,n和平面α,β,α⊥β的一个充分条件是(　　)

(A)m⊥n,m∥α,n∥β (B)m⊥n,α∩β=m,n?α

(C)m∥n,n⊥β,m?α (D)m∥n,m⊥α,n⊥β

设α,β表示两个不同平面,l,m表示两条不同的直线,则下列命题正确的是(　　)

(A)若l⊥m,l?α,m?β,则α⊥β

(B)若l⊥α,m∥β,α⊥β,则l⊥m

(C)若l∥m,l?α,m⊥β,则α∥β

(D)若l⊥α,m⊥β,α∥β,则l∥m

已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有(　　)

(A)0个 (B)1个 (C)2个 (D)3个

已知直线m,n和平面α,β满足m⊥n,m⊥α,α⊥β,则(　　)

(A)n⊥β (B)n∥β

(C)n⊥α (D)n∥α或n?α

如图,四边形ABCD中,AB=AD=CD=1,BD=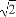,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是(　　)

(A)A'C⊥BD

(B)∠BA'C=90°

(C)CA'与平面A'BD所成的角为30°

(D)四面体A'-BCD的体积为

已知直线l⊥平面α,直线m?平面β,给出下列命题:①α∥β⇒l⊥m.②α⊥β⇒l∥m.③l∥m⇒α⊥β.④l⊥m⇒α∥β,其中正确命题的序号是　　　　.

若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则　　　　(写出所有正确结论的编号).

①四面体ABCD每组对棱相互垂直;

②四面体ABCD每个面的面积相等;

③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°;

④连接四面体ABCD每组对棱中点的线段相互垂直平分;

⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.