设互不相同的直线l,m,n和平面α,β,γ,给出下列三个命题:

①若l与m为异面直线,l?α,m?β,则α∥β;

②若α∥β,l?α,m?β,则l∥m;

③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.

其中真命题的个数为　　　　.

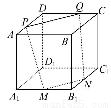
如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=　　　　.

已知平面α∥平面β,P是α,β外一点,过点P的直线m分别与α,β交于A,C,过点P的直线n分别与α,β交于B,D,且PA=6,AC=9,PD=8,则BD的长为　　　　.

如图,在正方体ABCD-A1B1C1D1中,E,F,G,M,N分别是B1C1,A1D1,A1B1,BD,B1C的中点,

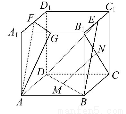
求证:(1)MN∥平面CDD1C1.

(2)平面EBD∥平面FGA.

在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.若M是线段AD的中点,

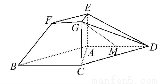
求证:GM∥平面ABFE.

如图所示,四边形EFGH所在平面为三棱锥A-BCD的一个截面,四边形EFGH为平行四边形.

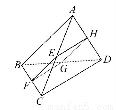
(1)求证:AB∥平面EFGH,CD∥平面EFGH.

(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.

如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点M在AD1上移动,点N在BD上移动,D1M=DN=a(0<a<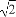),连接MN.

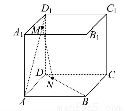
(1)证明对任意a∈(0,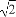),总有MN∥平面DCC1D1.

(2)当a为何值时,MN的长最小?

已知向量a=(2,-3,5)与向量b=(3,λ,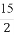)平行,则λ=(　　)

(A) (B) (C)- (D)-

设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k),若α∥β,则k等于(　　)

(A)2 (B)-4 (C)4 (D)-2

若平面α,β垂直,则下面可以是这两个平面的法向量的是(　　)

(A)n1=(1,2,1),n2=(-3,1,1)

(B)n1=(1,1,2),n2=(-2,1,1)

(C)n1=(1,1,1),n2=(-1,2,1)

(D)n1=(1,2,1),n2=(0,-2,-2)