
科目: 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:选择题
给出以下三个命题:
①将一枚硬币抛掷两次,记事件A:两次都出现正面,事件B:两次都出现反面,则事件A与事件B是对立事件;②在命题①中,事件A与事件B是互斥事件;③在10件产品中有3件是次品,从中任取3件,记事件A:所取3件中最多有2件是次品,事件B:所取3件中至少有2件是次品,则事件A与事件B是互斥事件.其中真命题的个数是( )
(A)0 (B)1 (C)2 (D)3
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:选择题
甲、乙两人下棋,和棋的概率为 ,乙获胜的概率为
,乙获胜的概率为 ,则下列说法正确的是( )
,则下列说法正确的是( )
(A)甲获胜的概率是
(B)甲不输的概率是
(C)乙输了的概率是
(D)乙不输的概率是
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:选择题
一个袋中装有大小相同,编号分别为1,2,3,4,5,6,7,8的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和小于15的概率为( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:填空题
袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,已知取到红球的概率是 ,取到黑球或黄球的概率是
,取到黑球或黄球的概率是 ,取到黄球或绿球的概率也是
,取到黄球或绿球的概率也是 ,则取到黑球、黄球、绿球的概率分别是 .
,则取到黑球、黄球、绿球的概率分别是 .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:填空题
从1,2,3,4这四个数中一次随机地取两个数,则其中一个数是另一个数的两倍的概率是 .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:填空题
盒子中共有除颜色不同其他均相同的3只红球,1只黄球,若从中随机取出两只球,则它们颜色不同的概率为 .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:填空题
甲、乙两颗卫星同时监测台风,在同一时刻,甲、乙两颗卫星准确预报台风的概率分别为0.8和0.75,则在同一时刻至少有一颗卫星预报准确的概率为 .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:填空题
某学校成立了数学、英语、音乐3个课外兴趣小组,3个小组分别有39,32,33个成员,一些成员参加了不止一个小组,具体情况如图所示.现随机选取一个成员,他属于至少2个小组的概率是 ,他属于不超过2个小组的概率是 .
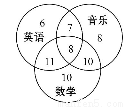
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:解答题
某校高三某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下图,据此解答如下问题:
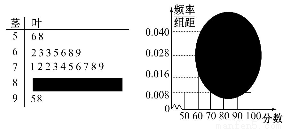
(1)求分数在[50,60)的频率及全班的人数.
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高.
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份在[90,100]之间的概率.
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业六十九第十章第六节练习卷(解析版) 题型:选择题
已知三棱锥S -ABC,在三棱锥内任取一点P,使得VP-ABC< VS-ABC的概率是( )
VS-ABC的概率是( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com