
科目: 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
点P(4,-2)与圆x2+y2=4上任一点连线的中点的轨迹方程是( )
(A)(x-2)2+(y+1)2=1 (B)(x-2)2+(y+1)2=4
(C)(x+4)2+(y-2)2=4 (D)(x+2)2+(y-1)2=1
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
)已知两点A(0,-3),B(4,0),若点P是圆x2+y2-2y=0上的动点,则△ABP面积的最小值为( )
(A)6 (B)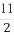 (C)8 (D)
(C)8 (D)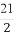
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
当a为任意实数时,直线(a-1)x-y+a+1=0恒过定点C,则以C为圆心,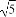 为半径的圆的方程为( )
为半径的圆的方程为( )
(A)x2+y2-2x+4y=0 (B)x2+y2+2x+4y=0
(C)x2+y2+2x-4y=0 (D)x2+y2-2x-4y=0
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:选择题
过点A(11,2)作圆x2+y2+2x-4y-164=0的弦,其中弦长为整数的共有( )
(A)16条 (B)17条 (C)32条 (D)34条
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:填空题
圆C:x2+y2+2x-2y-2=0的圆心到直线3x+4y+14=0的距离是 .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:填空题
已知方程x2+y2+kx+2y+k2=0所表示的圆有最大的面积,则直线y=(k-1)x+2的倾斜角α= .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:填空题
设二次函数y= x2-
x2- x+1与x轴正半轴的交点分别为A,B,与y轴正半轴的交点是C,则过A,B,C三点的圆的标准方程是 .
x+1与x轴正半轴的交点分别为A,B,与y轴正半轴的交点是C,则过A,B,C三点的圆的标准方程是 .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:填空题
设圆C同时满足三个条件:①过原点;②圆心在直线y=x
上;③截y轴所得的弦长为4,则圆C的方程是 .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上.圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
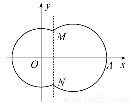
(1)求圆弧C2的方程.
(2)曲线C上是否存在点P,满足PA=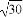 PO?若存在,指出有几个这样的点;若不存在,请说明理由.
PO?若存在,指出有几个这样的点;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业五十二第八章第三节练习卷(解析版) 题型:解答题
如图,
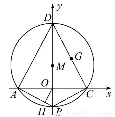
在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.
(1)求证:F<0.
(2)若四边形ABCD的面积为8,对角线AC的长为2,且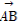 ·
·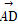 =0,求D2+E2-4F的值.
=0,求D2+E2-4F的值.
(3)设四边形ABCD的一条边CD的中点为G,OH⊥AB且垂足为H.试用平面解析几何的研究方法判断点O,G,H是否共线,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com