设数列{an}的前n项和为Sn,已知a1=1,Sn+1=2Sn+n+1(n∈N*),则数列{an}的通项公式an=　　　.

已知数列{an}中,a1=1,前n项和为Sn且Sn+1=Sn+1,n∈N*.

(1)求数列{an}的通项公式.

(2)求数列{}的前n项和Tn.

已知{an}是各项均为正数的等比数列,且a1+a2=2(+),a3+a4+a5=64(++),

(1)求{an}的通项公式.

(2)设bn=(an+)2,求数列{bn}的前n项和Tn.

已知数列{an}是等差数列,a2=6,a5=12,数列{bn}的前n项和是Sn,且Sn+bn=1.

(1)求数列{an}的通项公式.

(2)求证:数列{bn}是等比数列.

(3)记cn=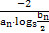,{cn}的前n项和为Tn,若Tn<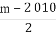对一切n∈N*都成立,求最小正整数m.

定义:若数列{An}满足An+1=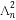,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.

(1)证明:数列{2an+1}是 “平方递推数列”,且数列{lg(2an+1)}为等比数列.

(2)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)…(2an+1),求数列{an}的通项公式及Tn关于n的表达式.

已知数列{an}满足a1=1,an=3n-1+an-1(n≥2).

(1)求a2,a3.(2)求通项公式an.

使a<b成立的一个充分不必要条件是(　　)

(A)a<b+1 (B)a<b-1

(C)> (D)a3<b3

若a,b是任意实数,且a>b,则 (　　)

(A)a2>b2 (B)<1

(C)lg(a-b)>0 (D)()a<()b

已知a,b为实数,则“a>b>1”是“<”的(　　)

(A)充分不必要条件 　　　　(B)必要不充分条件

(C)充分必要条件 　　　　(D)既不充分也不必要条件

已知P:a>b>0,Q:a2>b2,那么P是Q成立的(　　)

(A)充分不必要条件 　　　(B)必要不充分条件

(C)充分必要条件 　　　　(D)既不充分也不必要条件