
科目: 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:选择题
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数f(x)的图象恰好通过n(n∈N*)个整点,则称函数f(x)为n阶整点函数.有下列函数:
①f(x)=x+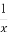 (x>0);②g(x)=x3;
(x>0);②g(x)=x3;
③h(x)=( )x;④φ()=lnx.
)x;④φ()=lnx.
其中是一阶整点函数的是( )
(A)①②③④ (B)①③④
(C)④ (D)①④
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:选择题
若在曲线f(x,y)=0上存在两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0的“自公切线”.下列方程:①x2-y2=1;②y=x2-|x|;③y=3sinx+4cosx;④|x|+1=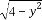 对应的曲线中存在“自公切线”的有( )
对应的曲线中存在“自公切线”的有( )
(A)①② (B)②③
(C)①④ (D)③④
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:填空题
观察下列等式:13+23=32,13+23+33=62,13+23+33+43=102,…,根据上述规律,第五个等式为 .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:填空题
设函数f(x)= (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= ,f2(x)=f(f1(x))=
,f2(x)=f(f1(x))=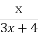 ,f3(x)=f(f2(x))=
,f3(x)=f(f2(x))= ,故fn(x)= .
,故fn(x)= .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:填空题
已知P(x0,y0)是抛物线y2=2px(p>0)上的一点,过P点的切线方程的斜率可通过如下方式求得:
在y2=2px两边同时求导,得:
2yy'=2p,则y'=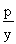 ,所以过P的切线的斜率:k=
,所以过P的切线的斜率:k=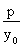 .
.
试用上述方法求出双曲线x2-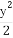 =1在P(
=1在P(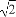 ,
,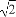 )处的切线方程为 .
)处的切线方程为 .
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:填空题
设等差数列{an}的前n项和为Sn,则S4,S8-S4,S12-S8,S16-S12成等差数列,类比以上结论有:设等比数列{bn}的前n项积为Tn,则T4, , ,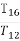 成等比数列.
成等比数列.
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:填空题
若集合A1,A2,…,An满足A1∪A2∪…∪An=A,则称A1,A2,…,An为集合A的一种拆分.已知:
①当A1∪A2={a1,a2,a3}时,有33种拆分;
②当A1∪A2∪A3={a1,a2,a3,a4}时,有74种拆分;
③当A1∪A2∪A3∪A4={a1,a2,a3,a4,a5}时,有155种拆分;
……
由以上结论,推测出一般结论:
当A1∪A2∪…∪An={a1,a2,a3,…,an+1}时,有 种拆分.
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:解答题
如图所示,底面为平行四边形ABCD的四棱锥P-ABCD中,E为PC的中点.求证:PA∥平面BDE.(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来)
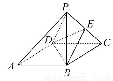
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:解答题
某少数民族的刺绣有着悠久的历史,如图(1)(2)(3)(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
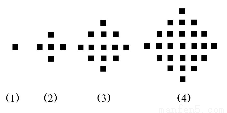
(1)求出f(5).
(2)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的关系式.
查看答案和解析>>
科目: 来源:2014年高考数学全程总复习课时提升作业三十二第五章第三节练习卷(解析版) 题型:选择题
已知等比数列{an}的公比q=2,其前4项和S4=60,则a2等于( )
(A)8(B)6(C)-8(D)-6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com