随机变量η的分布列如下:

则①x=　　　　　;②P(η>3)=　　　　　;

③P(1<η≤4)=　　　　　.

某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是,,且各轮次通过与否相互独立.

(1)设该选手参赛的轮次为ξ,求ξ的分布列.

(2)对于(1)中的ξ,设“函数f(x)=3sinπ(x∈R)是偶函数”为事件D,求事件D发生的概率.

现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.

(1)求该射手恰好命中一次的概率.

(2)求该射手的总得分X的分布列.

一个袋中装有若干个大小相同的黑球、白球和红球,已知从袋中任意摸出1个球,得到黑球的概率是;从袋中任意摸出2个球,至少得到1个白球的概率是.

(1)若袋中共有10个球,

①求白球的个数;

②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.

(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于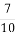,并指出袋中哪种颜色的球的个数最少.

将下列各极坐标方程化为直角坐标方程.

(1)θ=(ρ∈R).　(2)ρcos2=1.

求经过极点O(0,0),A(6,),B(6,)三点的圆的极坐标方程.

已知☉O1和☉O2的极坐标方程分别是ρ=2cosθ和ρ=2asinθ(a是非零常数).

(1)将两圆的极坐标方程化为直角坐标方程.

(2)若两圆的圆心距为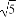,求a的值.

求过点A(3,)且和极轴成角的直线.

已知曲线C:ρsin(θ+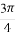)=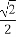,曲线P:ρ2-4ρcosθ+3=0,

(1)求曲线C,P的直角坐标方程.

(2)设曲线C和曲线P的交点为A,B,求|AB|.

在极坐标系(ρ,θ)(0≤θ<2π)中,求曲线ρ=2sinθ与ρcosθ=1的交点Q的极坐标.