
科目: 来源:月考题 题型:解答题
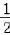 ,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间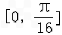 上的最小值.
上的最小值. 查看答案和解析>>
科目: 来源:月考题 题型:单选题
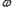 x+
x+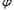 )(
)(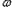 >0,0<
>0,0<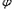 ≤
≤ ),且此函数的图象如图所示,由点P(
),且此函数的图象如图所示,由点P(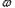 ,
,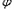 )的坐标是
)的坐标是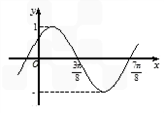
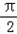 )
)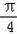 )
)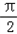 )
)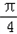 )
)查看答案和解析>>
科目: 来源:高考真题 题型:解答题
 =(cosωx-sinωx,sinωx),
=(cosωx-sinωx,sinωx), =(-cosωx-sinωx,2
=(-cosωx-sinωx,2 cosωx),设函数f(x)=
cosωx),设函数f(x)=
 +λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ,1)。
,1)。 ,0)求函数f(x)在区间[0,
,0)求函数f(x)在区间[0, ]上的取值范围。
]上的取值范围。查看答案和解析>>
科目: 来源:月考题 题型:单选题
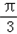 )的图象,只需把函数y=sin(2x+
)的图象,只需把函数y=sin(2x+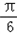 )的图象
)的图象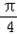 个长度单位
个长度单位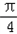 个长度单位
个长度单位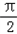 个长度单位
个长度单位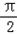 个长度单位
个长度单位查看答案和解析>>
科目: 来源:期末题 题型:解答题
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com