
科目: 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:选择题
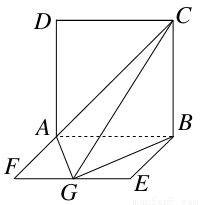
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=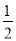 AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
A. B.
B.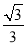 C.
C.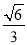 D.
D.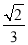
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:选择题
如图所示,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.当A1、E、F、C1共面时,平面A1DE与平面C1DF所成二面角的余弦值为( )
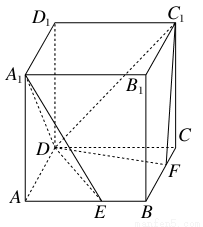
A.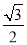 B.
B.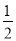 C.
C.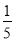 D.
D.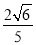
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:选择题
如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹为( )
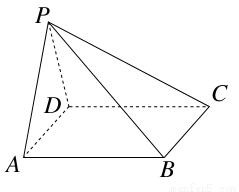
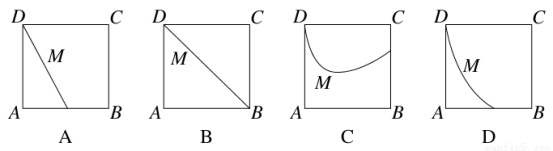
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:填空题
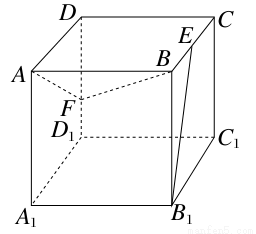
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是棱BC、DD1上的点,如果B1E⊥平面ABF,则CE与DF的和的值为________.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:填空题
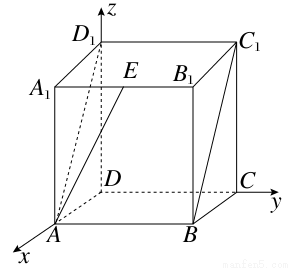
已知棱长为1的正方体ABCD-A1B1C1D1中,E是A1B1的中点,则直线AE与平面ABC1D1所成角的正弦值为________.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:填空题
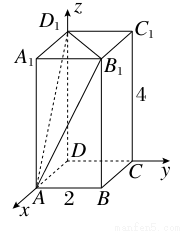
已知在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是________.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:填空题
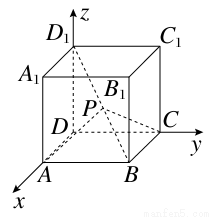
设动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,记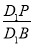 =λ.当∠APC为钝角时,λ的取值范围是________.
=λ.当∠APC为钝角时,λ的取值范围是________.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:解答题
如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.
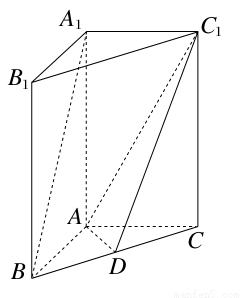
(1)求异面直线A1B与C1D所成角的余弦值;
(2)求平面ADC1与平面ABA1夹角的正弦值.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:解答题
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
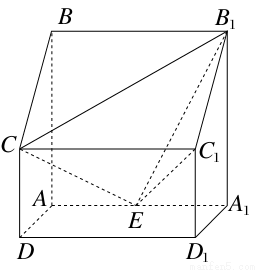
(1)证明:B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为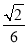 ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:解答题
如下图所示,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°.
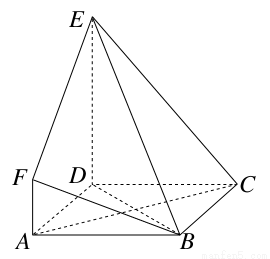
(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com