
科目: 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:解答题
在如图所示的几何体中,正方形ABCD和矩形ABEF所在的平面互相垂直,M为AF的中点,BN⊥CE.
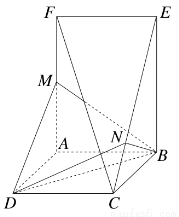
(1)求证:CF∥平面MBD;
(2)求证:CF⊥平面BDN.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:选择题
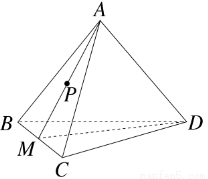
如图,在棱长为4的正四面体A-BCD中,M是BC的中点,点P在线段AM上运动(P不与A,M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥平面AMD;②Q点一定在直线DM上;③VC-AMD=4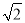 .
.
其中正确命题的序号是( )
A.①② B.①③ C.②③ D.①②③
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:填空题
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)

查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:解答题
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面PAD⊥平面ABCD,且∠DAB=60°,AB=2,E为AD的中点.

(1)求证:AD⊥PB;
(2)求点E到平面PBC的距离.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:选择题
已知向量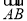 =(2,4,5),
=(2,4,5), =(3,x,y),若
=(3,x,y),若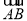 ∥
∥ ,则( )
,则( )
A.x=6,y=15 B.x=3,y=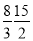
C.x=3,y=15 D.x=6,y=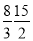
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:选择题
已知正方体ABCD-A1B1C1D1中,点E为上底面A1C1的中心,若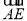 =
=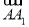 +x
+x +y
+y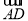 ,则x、y的值分别为( )
,则x、y的值分别为( )
A.x=1,y=1 B.x=1,y=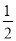
C.x=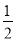 ,y=
,y=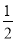 D.x=
D.x= ,y=1
,y=1
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:选择题
已知平面α内有一个点A(2,-1,2),α的一个法向量为n=(3,1,2),则下列点P中,在平面α内的是( )
A.(1,-1,1) B.(1,3, )
)
C.(1,-3, ) D.(-1,3,-
) D.(-1,3,-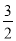 )
)
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:选择题
△ABC的顶点分别为A(1,-1,2),B(5,-6,2),C(1,3,-1),则AC边上的高BD等于( )
A.5 B.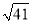 C.4 D.2
C.4 D.2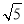
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:选择题
如图所示,已知空间四边形OABC中,|OB|=|OC|,且∠AOB=∠AOC,则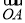 、
、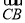 夹角θ的余弦值为( )
夹角θ的余弦值为( )

A.0 B.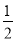 C.
C.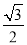 D.
D.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:选择题
如图,正方体ABCD-A1B1C1D1中,E,F分别在A1D,AC上,且A1E=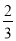 A1D,AF=
A1D,AF= AC,则( )
AC,则( )
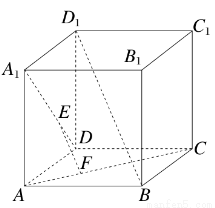
A.EF至多与A1D,AC之一垂直
B.EF⊥A1D,EF⊥AC
C.EF与BD1相交
D.EF与BD1异面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com