分析法又称执果索因法，若用分析法证明：“设a>b>c，且a＋b＋c＝0，求证 <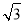a”索的因应是(　　)

A．a－b>0 B．a－c>0

C．(a－b)(a－c)>0 D．(a－b)(a－c)<0

设x，y，z>0，则三个数＋，＋，＋ (　　)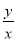

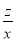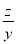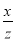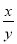A．都大于2 B．至少有一个大于2

C．至少有一个不小于2 D．至少有一个不大于2

设a，b是两个实数，给出下列条件：

①a＋b>1；②a＋b＝2；③a＋b>2；④a2＋b2>2；⑤ab>1.

其中能推出：“a，b中至少有一个大于1”的条件是(　　)

A．②③ B．①②③ C．③ D．③④⑤

用反证法证明某命题时，对结论：“自然数a，b，c中恰有一个偶数”正确的反设为(　　)

A．a，b，c中至少有两个偶数

B．a，b，c中至少有两个偶数或都是奇数

C．a，b，c都是奇数

D．a，b，c都是偶数

不相等的三个正数a、b、c成等差数列，并且x是a、b的等比中项，y是b、c的等比中项，则x2、b2、y2三数(　　)

A．成等比数列而非等差数列

B．成等差数列而非等比数列

C．既成等差数列又成等比数列

D．既非等差数列又非等比数列

若a，b，c是不全相等的正数，给出下列判断：

①(a－b)2＋(b－c)2＋(c－a)2≠0；

②a>b与a<b及a＝b中至少有一个成立；

③a≠c，b≠c，a≠b不能同时成立．

其中判断正确的是________．

请阅读下列材料：若两个正实数a1，a2满足a12＋a22＝1，那么a1＋a2≤.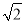

证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤.

根据上述证明方法，若n个正实数满足a12＋a22＋…＋an2＝1时，你能得到的结论为________．

已知x∈R，a＝x2＋，b＝2－x，c＝x2－x＋1，试证明a，b，c至少有一个不小于1.

已知函数f(x)＝ax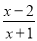＋ (a>1)．

(1)证明：函数f(x)在(－1，＋∞)上为增函数；

(2)用反证法证明方程f(x)＝0没有负数根．

已知非零向量a，b，且a⊥b，求证：≤.