
科目: 来源:2015高考数学(理)一轮配套特训:3-3三角函数的图象与性质(解析版) 题型:解答题
已知函数f(x)=2cosxsin(x+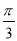 )-
)- sin2x+sinxcosx.
sin2x+sinxcosx.
(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象沿x轴向右平移m个单位后的图象关于直线x=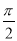 对称,求m的最小正值.
对称,求m的最小正值.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
将函数f(x)=sin(2x+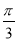 )的图象向左平移φ个单位,得到偶函数g(x)的图象,则φ的最小正值为( )
)的图象向左平移φ个单位,得到偶函数g(x)的图象,则φ的最小正值为( )
A.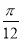 B.
B.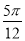 C.
C.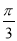 D.
D.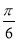
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
已知函数y=Asin(ωx+φ)+k的最大值是4,最小值是0,最小正周期是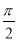 ,直线x=
,直线x=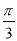 是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
A.y=4sin(4x+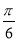 ) B.y=2sin(2x+
) B.y=2sin(2x+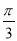 )+2
)+2
C.y=2sin(4x+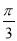 )+2 D.y=2sin(4x+
)+2 D.y=2sin(4x+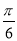 )+2
)+2
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
函数y=Asin(ωx+φ)(ω>0,|φ|≤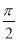 )的部分图象如图所示,则函数的一个表达式为( )
)的部分图象如图所示,则函数的一个表达式为( )
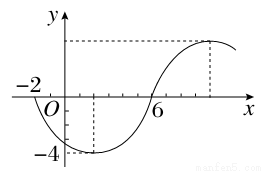
A.y=-4sin(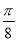 x+
x+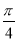 )
)
B.y=4sin( x-
x-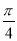 )
)
C.y=-4sin( x-
x-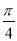 )
)
D.y=4sin(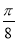 x+
x+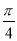 )
)
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
函数f(x)=sin(ωx+φ)(ω>0,|φ|<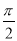 )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移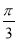 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点(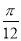 ,0)对称 B.关于直线x=
,0)对称 B.关于直线x=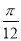 对称
对称
C.关于点(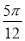 ,0)对称 D.关于直线x=
,0)对称 D.关于直线x=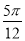 对称
对称
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
要得到函数y=3sin(2x+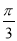 )的图象,只需要将函数y=3cos2x的图象( )
)的图象,只需要将函数y=3cos2x的图象( )
A.向右平移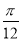 个单位 B.向左平移
个单位 B.向左平移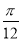 个单位
个单位
C.向右平移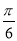 个单位 D.向左平移
个单位 D.向左平移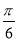 个单位
个单位
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:选择题
已知函数f(x)=Asin(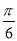 x+φ)(A>0,0<φ<
x+φ)(A>0,0<φ<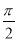 )的部分图象如图所示,P,Q分别为该图象的最高点和最低点,点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=
)的部分图象如图所示,P,Q分别为该图象的最高点和最低点,点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=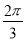 ,则y=f(x)的最大值及φ的值分别是( )
,则y=f(x)的最大值及φ的值分别是( )
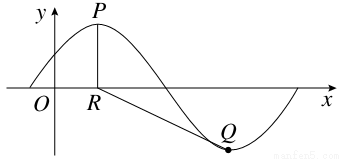
A.2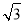 ,
,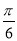 B.
B.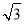 ,
,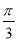
C.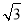 ,
,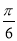 D.2
D.2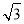 ,
,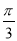
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:填空题
若将函数y=sin(ωx+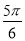 )(ω>0)的图象向右平移
)(ω>0)的图象向右平移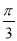 个单位长度后,与函数y=sin(ωx+
个单位长度后,与函数y=sin(ωx+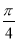 )的图象重合,则ω的最小值为________.
)的图象重合,则ω的最小值为________.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:填空题
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)的值为________.
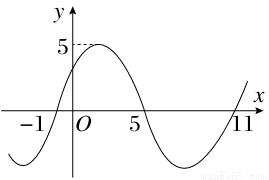
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:3-4正弦型函数的图象及应用(解析版) 题型:填空题
已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<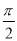 ),y=f(x)的部分图象如图所示,则f(
),y=f(x)的部分图象如图所示,则f(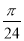 )=________.
)=________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com