
科目: 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:填空题
设随机变量的概率分布为
ε | 0 | 1 | 2 |
P |
|
| 1- |
则ξ的数学期望的最小值是________.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:填空题
盒中有9个正品、3个次品零件,每次取1个零件,如果取出的次品不再放回,则在取得正品前已取出的次品数ξ的分布列________.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:填空题
某学生在参加政、史、地三门课程的学业水平考试中,取得A等级的概率分别为 、
、 、
、 ,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望E(ξ)的值为________.
,且三门课程的成绩是否取得A等级相互独立.记ξ为该生取得A等级的课程数,其分布列如表所示,则数学期望E(ξ)的值为________.
ξ | 0 | 1 | 2 | 3 |
P |
| a | b |
|
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:解答题
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率;
(2)求ξ的分布列.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:解答题
袋中共有10个大小相同的编号为1,2,3的球,其中1号球有1个,2号球有m个,3号球有n个.从袋中依次摸出2个球,已知在第一次摸出3号球的前提下,再摸出一个2号球的概率是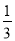 .
.
(1)求m,n的值;
(2)从袋中任意摸出2个球,设得到小球的编号数之和为ξ,求随机变量ξ的分布列.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:解答题
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3题,每人答对其中2题就停止答题,即闯关成功.已知在6道被选题中,甲能答对其中的4道题,乙答对每道题的概率都是.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为ξ,求ξ的分布列.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:选择题
一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a,b,c∈(0,1)),已知他投篮一次得分的均值为2,则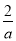 +
+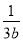 的最小值为( )
的最小值为( )
A.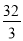 B.
B.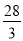 C.
C.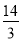 D.
D.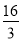
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:填空题
装有某种产品的盒中有7件正品,3件次品,无放回地每次取一件产品,直至抽到正品为止,已知抽取次数ξ为随机变量,则抽取次数ξ的数学期望E(ξ)=________.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:填空题
某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历.假定该毕业生得到甲公司面试的概率为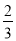 ,得到乙、丙两公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记X为该毕业生得到面试的公司个数.若P(X=0)=
,得到乙、丙两公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记X为该毕业生得到面试的公司个数.若P(X=0)=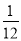 ,则随机变量X的数学期望E(X)=________.
,则随机变量X的数学期望E(X)=________.
查看答案和解析>>
科目: 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:解答题
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com