设曲线C的参数方程为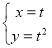 (t为参数)，若以直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，则曲线C的极坐标方程为_______________．

函数=的最小值为________________．

展开式中的常数项是_________________.

将三个分别标有A，B，C的球随机放入编号为1,2,3,4的四个盒子中，则1号盒子中有球的不同放法种数为______________．

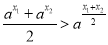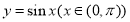已知点是函数的图象上任意不同两点，依据图象可知，线段AB总是位于A、B两点之间函数图象的上方，因此有结论成立．运用类比思想方法可知，若点是函数的图象上任意不同两点，则类似地有_________________成立．

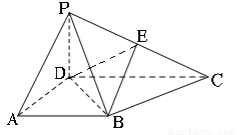
如图，在四棱锥P?ABCD中，PD⊥平面ABCD，AB∥CD，AD⊥CD，且AB=AD=PD=1，CD=2，E为PC的中点．

（1）求证：BE∥平面PAD；

（2）求二面角E?BD?C的余弦值．

小王经营一家面包店，每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元，若当天卖不完，则未卖出的现烤面包因过期每个亏损5元.经统计，得到在某月（30天）中，小王每天售出的现烤面包个数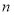及天数如下表：

试依据以频率估计概率的统计思想，解答下列问题：

（1）计算小王某天售出该现烤面包超过13个的概率；

（2）若在今后的连续5天中，售出该现烤面包超过13个的天数大于3天，则小王决定增加订购量.试求小王增加订购量的概率.

（3）若小王每天订购14个该现烤面包，求其一天出售该现烤面包所获利润的分布列和数学期望.

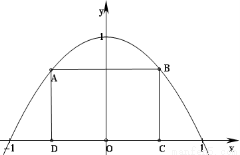
如图所示，抛物线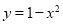与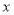轴所围成的区域是一块等待开垦的土地，现计划在该区域内围出一块矩形地块ABCD作为工业用地，其中A、B在抛物线上，C、D在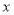轴上.已知工业用地每单位面积价值为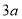元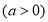，其它的三个边角地块每单位面积价值元.

（1）求等待开垦土地的面积；

（2）如何确定点C的位置，才能使得整块土地总价值最大.

已知曲线C上任意一点P到两定点F1(?1,0)与F2(1,0)的距离之和为4．

（1）求曲线C的方程；

（2）设曲线C与x轴负半轴交点为A，过点M(?4,0)作斜率为k的直线l交曲线C于B、C两点（B在M、C之间），N为BC中点．

(ⅰ)证明：k·kON为定值；

(ⅱ)是否存在实数k，使得F1N⊥AC？如果存在，求直线l的方程，如果不存在，请说明理由．

已知函数f(x)=ln(x+1)+ax2?x，a∈R．

（1）当时，求函数y=f(x)的极值；

（2）是否存在实数b∈(0,1)，使得当x∈(?1,b]时，函数f(x)的最大值为f(b)？若存在，求实数a的取值范围，若不存在，请说明理由．