练习册

  • 练习册
  • 试题
    相关习题
     0  20044  20052  20058  20062  20068  20070  20074  20080  20082  20088  20094  20098  20100  20104  20110  20112  20118  20122  20124  20128  20130  20134  20136  20138  20139  20140  20142  20143  20144  20146  20148  20152  20154  20158  20160  20164  20170  20172  20178  20182  20184  20188  20194  20200  20202  20208  20212  20214  20220  20224  20230  20238  266669 

    科目： 来源：0119 月考题 题型：解答题

    设C1，C2，…，Cn，…是坐标平面上的一列圆，它们的圆心都在x轴的正半轴上，且都与直线y=x相切，对每一个正整数n，圆Cn都与圆Cn+1相互外切，以rn表示Cn的半径，已知{rn}为递增数列。
    （Ⅰ）证明：{rn}为等比数列；
    （Ⅱ）设r1=1，求数列的前n项和。

    查看答案和解析>>

    科目： 来源：0118 月考题 题型：解答题

    如果有穷数列a1，a2，a3，…，am（m为正整数）满足条件a1=am，a2=am-1，…，am=a1，即ai=am-i+1（i=1，2，…，m），我们称其为“对称数列”。
    例如，数列1，2，5，2，1与数列8，4，2，2，4，8都是“对称数列”。 
    （1）设{bn}是7项的“对称数列”，其中b1，b2，b3，b4是等差数列，且b1=2，b4=11，依次写出{bn}的每一项；
    （2）设{cn}是49项的“对称数列”，其中c25，c26，…，c49是首项为1，公比为2的等比数列，求{cn}各项的和S；
    （3）设{an}是100项的“对称数列”，其中d51，d52，…，d100是首项为2，公差为3的等差数列，求{dn}前n项的和Sn（n=1，2，…，100）。

    查看答案和解析>>

    科目： 来源：0118 月考题 题型：填空题

    若对任意的自然数n，，则n=（    ）。

    查看答案和解析>>

    科目： 来源：0118 月考题 题型：填空题

    已知数列{an}的前n项和为Sn，对任意n∈N*，都有，且1＜Sk＜9，则a1的值为（    ），k的值为（    ）。

    查看答案和解析>>

    科目： 来源：0118 月考题 题型：解答题

    已知{an}是等差数列，公差d＞0，a2，a5是方程x2-12x+27=0的两根，数列{bn}的前n项和为Tn，且Tn=1-bn（n∈N*）。
    (1)求数列{an}，{bn}的通项公式；
    (2)记c=anbn，求数列{cn}的前n项和Sn。

    查看答案和解析>>

    科目： 来源：0118 月考题 题型：解答题

    已知数列{an}中，a1=3，an+1-2an=0，数列{bn}中，bn·an=（-1）n（n∈N*）。
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）求数列{bn}的通项公式以及前n项的和。

    查看答案和解析>>

    科目： 来源：0104 月考题 题型：解答题

    等差数列{an}的各项均为正数，a1=3，前n项和为Sn，{bn}为等比数列，b1=2，且b2S2=32，b3S3=120。 （1）求an与bn；
    （2）求数列{anbn}的前n项和Tn；
    （3）若对任意正整数n和任意x∈R恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目： 来源：0112 模拟题 题型：单选题

    若数列{an}对于任意的正整数n满足：an＞0且anan+1=n+1，则称数列{an}为“积增数列”。已知“积增数列”{an}中，a1=1，数列{an2+an+12}的前n项和为Sn，则对于任意的正整数n，有

    [     ]

    A、Sn≤2n2+3
    B、Sn≥n2+4n
    C、Sn≤n2+4n
    D、Sn≥n2+3n

    查看答案和解析>>

    科目： 来源：0112 模拟题 题型：解答题

    已知数列{an}满足：a1=1，a2=a（a＞0），数列{bn}满足bn=anan+1（n∈N*）。
    （Ⅰ）若{an}是等差数列，且b3=12，求数列{an}的通项公式；
    （Ⅱ）若{an}是等比数列，求数列{bn}的前n项和Sn；
    （Ⅲ）若{bn}是公比为a-1的等比数列时，{an}能否为等比数列？若能，求出a的值；若不能，请说明理由。

    查看答案和解析>>

    科目： 来源：广东省模拟题 题型：解答题

    设Sn为数列{an}的前n项和，对任意的n∈N*，都有Sn=（m+1）-man（m为常数，且m＞0）。
    （1）求证：数列{an}是等比数列；
    （2）设数列{an}的公比q=f（m），数列{bn}满足b1=2a1，bn=f（bn-1）（n≥2，n∈N*），求数列{bn}的通项公式；
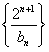    （3）在满足（2）的条件下，求数列的前n项和Tn。

    查看答案和解析>>

    同步练习册答案