练习册

  • 练习册
  • 试题
    相关习题
     0  210499  210507  210513  210517  210523  210525  210529  210535  210537  210543  210549  210553  210555  210559  210565  210567  210573  210577  210579  210583  210585  210589  210591  210593  210594  210595  210597  210598  210599  210601  210603  210607  210609  210613  210615  210619  210625  210627  210633  210637  210639  210643  210649  210655  210657  210663  210667  210669  210675  210679  210685  210693  266669 

    科目： 来源： 题型：

    从一箱产品中随机地抽取一件产品，设事件A=“抽到的一等品”，事件B=“抽到的二等品”，事件C=“抽到的三等品”，且已知P（A）=0.7，P（B）=0.1，P（C）=0.05，求下列事件的概率：
    （1）事件D=“抽到的是一等品或二等品”；
    （2）事件E=“抽到的是二等品或三等品”

    查看答案和解析>>

    科目： 来源： 题型：

    化简：
    sin(
    π
    2
    +α)cos(
    π
    2
    -α)
    cos(π+α)
    +
    sin(π-α)cos(
    π
    2
    +α)
    sin(π+α)
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    已知点F是椭圆C的右焦点，A，B是椭圆短轴的两个端点，且△ABF是正三角形，
    （Ⅰ）求椭圆C的离心率；
    （Ⅱ）直线l与以AB为直径的圆O相切，并且被椭圆C截得的弦长的最大值为2
    		3
    ，求椭圆C的标准方程．

    查看答案和解析>>

    科目： 来源： 题型：

    在锐角△ABC中，角A，B，C的对边分别为a，b，c，且满足cos2A-cos2B=cos（
    π
    6
    -A）cos（
    π
    6
    +A）．
    （Ⅰ）求角B的值；
    （Ⅱ）若b=1，且b＜a，求a+c的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    如图，已知抛物线C的顶点在原点，开口向右，过焦点且垂直于抛物线对称轴的弦长为2，过C上一点A作两条互相垂直的直线交抛物线于P，Q两点．
    （Ⅰ）若直线PQ过定点T（3，-
    		2
    ），求点A的坐标；
    （Ⅱ）对于第（Ⅰ）问的点A，三角形APQ能否为等腰直角三角形？若能，试确定三角形APD的个数；若不能，说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    已知等差数列{an}的各项均为正数，a1=3，前n项和为Sn，数列{bn}为等比数列，b1=1，且b2S2=4，b3S3=
    15
    4
    ．
    （1）求an与bn；
    （2）记数列（
    1
    Sn
    ）的前n项和为Tn，且
    lim
    n→∞
    Tn=T，求使bn≥
    T
    3
    成立的所有正整数n．

    查看答案和解析>>

    科目： 来源： 题型：

    设复数z=a+bi（a，b∈R，a＞0），满足|z|=
    		10
    ，且复数（1-2i）z在复平面上对应的点在第二、四象限的角平分线上．
    （Ⅰ）求复数z；
    （Ⅱ）若
    .
    z
    +
    m+i
    1-i
    （m∈R）为纯虚数，求实数m的值．

    查看答案和解析>>

    科目： 来源： 题型：

    椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）焦距为2
    		2
    ，且过点（
    		2
    ，1），动直线l和椭圆C相交于A，B两点，点N为线段AB的中点．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）当N的坐标为（1，1）时，求此时△AOB的面积；
    （Ⅲ）设点M也是椭圆C上的一点，且满足
    OM
    =
    3
    5
    OA
    +
    4
    5
    OB
    ，问：是否存在两个定点F1，F2使|NF1|+|NF2|为定值？若存在，求出的坐标；若不存在，则说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    如图，三棱柱ABC-A1B1C1中，CC1=BC1=
    		2
    ，BC=2，△ABC是以BC为底边的等腰三角形，平面ABC⊥平面BCC1B1，E、F分别为棱AB、CC1的中点．
    （1）求证：EF∥平面A1BC1
    （2）若AC≤CC1，且EF与平面ACC1A1所成的角的正弦值为
    		2
    3
    ，求二面角C-AA1-B的余弦值．

    查看答案和解析>>

    科目： 来源： 题型：

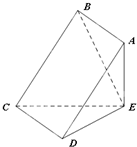    如图，E是平面ABCD外一点，AE⊥平面CDE．若四边形ABCD是正方形，M，N分别是AE，BC的中点．
    （Ⅰ）求证：平面ABCD⊥平面ADE；
    （Ⅱ）求证：MN∥平面CDE；
    （Ⅲ）若二面角B-CD-E的平面角的大小为30°，求BD与平面AEC所成角的正弦值．

    查看答案和解析>>

    同步练习册答案