科目： 来源： 题型：

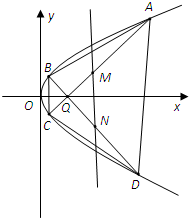已知抛物线y²=2px（p＞0）上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1． 
（Ⅰ）求p的值；
（Ⅱ）如图所示，过定点Q（2，0）且互相垂直的两条直线l₁、l₂分别与该抛物线分别交于A、C、B、D四点．
（i）求四边形ABCD面积的最小值；
（ii）设线段AC、BD的中点分别为M、N两点，试问：直线MN是否过定点？若是，求出定点坐标；若不是，请说明理由．

科目： 来源： 题型：

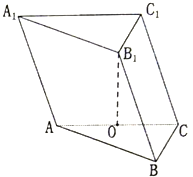已知三棱柱ABC-A₁B₁C₁的各条棱长均为2，点B₁在平面ABC内的射影恰好落在AC边的中点O处．
（1）求点A到平面BCC₁B₁的距离；
（2）棱BB₁上是否存在点P，使得二面角P-AC-B的大小为60°？若存在，请确定点P的位置；若不存在，请说明理由．

科目： 来源： 题型：

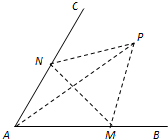如图，经过村庄A有两条夹角为60°的公路AB，AC，根据规划拟在两条公路之间的区域内建一工厂P，分别在两条公路边上建两个仓库M、N （异于村庄A），要求PM=PN=MN=2（单位：千米）．设∠AMN=θ．
（1）在△AMN和△AMP中试用θ表示AM和AP²；
（2）设AP²=f（θ），化简f（θ）；
（3）θ为多少时，工厂产生的噪声对居民的影响最小（即工厂与村庄的距离AP最远），并求出AP的最大值．

科目： 来源： 题型：

科目： 来源： 题型：

科目： 来源： 题型：

科目： 来源： 题型：

科目： 来源： 题型：

科目： 来源： 题型：

如图，在三棱锥P-ABC中，PA=PB=AB=BC，∠PBC=90°，D为AC的中点，AB⊥PD．
（1）求证：平面PAB⊥平面ABC；
（2）求二面角B-PD-C的余弦值．

科目： 来源： 题型：

在Rt△AOB中，∠OAB=

π

6

，斜边AB=4．Rt△AOB以直线AO为轴旋转得到Rt△AOC，且二面角B-AO-C是直二面角．动点D在斜边AB上．
（1）求证：平面COD⊥平面AOB；
（2）当AD=

1

2

DB时，求异面直线AO与CD所成角的正切值；
（3）求CD与平面AOB所成最大角的正切值．