练习册

  • 练习册
  • 试题
    相关习题
     0  211062  211070  211076  211080  211086  211088  211092  211098  211100  211106  211112  211116  211118  211122  211128  211130  211136  211140  211142  211146  211148  211152  211154  211156  211157  211158  211160  211161  211162  211164  211166  211170  211172  211176  211178  211182  211188  211190  211196  211200  211202  211206  211212  211218  211220  211226  211230  211232  211238  211242  211248  211256  266669 

    科目： 来源： 题型：

    设集合M={y|y=2sinx，x∈[-
    π
    2
    ，
    π
    2
    ]}，N={x|y=log2（x-1）}，则M∩N=（　　）
    A、{x|1＜x≤5}
    B、{x|-1＜x≤0}
    C、{x|-2≤x≤0}
    D、{x|1＜x≤2}

    查看答案和解析>>

    科目： 来源： 题型：

    已知i为虚数单位，则复数
    (2+i)(1-i)2
    1-2i
    等于（　　）
    A、2B、-2C、2iD、-2i

    查看答案和解析>>

    科目： 来源： 题型：

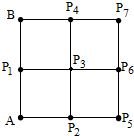    如图，四个边长为1的小正方形排成一个大正方形，AB是大正方形的一条边，Pi（i=1，2，…，7）是小正方形的其余顶点，则
    AB
    •
    APi
    （i=1，2，…，7）的不同值的个数为（　　）
    A、7B、5C、3D、1

    查看答案和解析>>

    科目： 来源： 题型：

    已知双曲线C：
    x2
    a2
    -
    y2
    b2
    =1（a＞0，b＞0）离心率为3，直线y=2与双曲线C的两个交点间的距离为
    		6
    ，则双曲线C的方程是（　　）
    A、2x2-y2=1
    B、x2-
    y2
    8
    =1
    C、
    x2
    5
    -
    y2
    10
    =1
    D、
    4x2
    5
    -
    y2
    10
    =1

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f（x）=1+x-
    x2
    2
    +
    x3
    3
    -
    x4
    4
    +…+
    x2013
    2013
    ，g（x）=1-x+
    x2
    2
    -
    x3
    3
    +
    x4
    4
    -…-
    x2013
    2013
    ．设 F（x）=f（x+4）．g（x-4），且函数F（x）的零点在区间[a-1，a]或[b-1，b]（a＜b，a，b∈Z）内，则a+b的值为（　　）
    A、-1B、0C、1D、2

    查看答案和解析>>

    科目： 来源： 题型：

    两名学生参加考试，随机变量x代表通过的学生数，其分布列为
    x012
    p
    1
    3
    1
    2
    1
    6
    那么这两人通过考试的概率最小值为（　　）
    A、
    1
    6
    B、
    1
    3
    C、
    1
    2
    D、
    2
    3

    查看答案和解析>>

    科目： 来源： 题型：

    小乐与小波在学了变量的相关性之后，两人约定回家去利用自己各自记录的6-10岁的身高记录作为实验数据，进行回归分析，探讨年龄x（岁）与身高y（cm）之间的线性相关性．经计算小乐与小波求得的线性回归直线分别为l1，l2，在认真比较后，两人发现他们这五年身高的平均值都为110cm，而且小乐的五组实验数据均满足所求的直线方程，小波则只有两组实验数据满足所求直线方程．下列说法错误的是（　　）
    A、直线l1，l2一定有公共点（8，110）
    B、在两人的回归分析中，小乐求得的线性相关系数r=1，小波求得的线性相关系数r∈（0，1）
    C、在小乐的回归分析中，他认为x与y之间完全线性相关，所以自己的身高y（cm）与年龄x（岁）成一次函数关系，利用l1可以准确预测自己20岁的身高
    D、在小波的回归分析中，他认为x与y之间不完全线性相关，所以自己的身高y（cm）与年龄x（岁）成相关关系，利用l2只可以估计预测自己20岁的身高

    查看答案和解析>>

    科目： 来源： 题型：

    已知曲线C为三次函数f（x）=3x-x3的图象，过点M（2，1）作曲线C的切线，可能的切线条数是（　　）
    A、0B、1C、2D、3

    查看答案和解析>>

    科目： 来源： 题型：

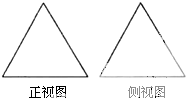    如图是两个全等的正三角形，给定下列三个命题：①存在四棱锥，其正视图、侧视图如图；②存在三棱锥，其正视图、侧视图如图；③存在圆锥，其正视图、侧视图如图．其中真命题的个数是（　　）
    A、3B、2C、1D、0

    查看答案和解析>>

    科目： 来源： 题型：

    已知两不重合直线a、b及两不重合平面α、β，那么下列命题中正确的是（　　）
    A、
    a∥α
    a∥β
    ⇒α∥β
    B、
    a∥α
    α∥β
    ⇒a∥β
    C、
    a⊥α
    β⊥α
    a?β
    ⇒a∥β
    D、
    a⊥α
    b⊥β
    ⇒a⊥b

    查看答案和解析>>

    同步练习册答案