练习册

  • 练习册
  • 试题
    相关习题
     0  211074  211082  211088  211092  211098  211100  211104  211110  211112  211118  211124  211128  211130  211134  211140  211142  211148  211152  211154  211158  211160  211164  211166  211168  211169  211170  211172  211173  211174  211176  211178  211182  211184  211188  211190  211194  211200  211202  211208  211212  211214  211218  211224  211230  211232  211238  211242  211244  211250  211254  211260  211268  266669 

    科目： 来源： 题型：

    如图，在△ABC中，∠C=45°，D为BC中点，BC=2．记锐角∠ADB=α．且满足cosα=-
    7
    25
    ．
    （1）求cos∠CAD；
    （2）求BC边上高的值．

    查看答案和解析>>

    科目： 来源： 题型：

    若复数z1=a+i，z2=1-i（i为虚数单位），且z1•z2为纯虚数，则实数a的值为
     
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    圆心在原点上与直线x+y-2=0相切的圆的方程为
     
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    在△ABC中，角A，B，C对应边分别是a，b，c，c=2，sin2A+sin2B-sin2C=sinAsinB．
    （1）若sinC+sin（B-A）=2sin2A，求△ABC面积；
    （2）求AB边上的中线长的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    某工厂某种产品的年产量为1000x件，其中x∈[20，100]，需要投入的成本为C（x），当x∈[20，80]时，C（x）=
    1
    2
    x2-30x+500（万元）；当x∈（80，100]时，C（x）=
    20000
    		x
    （万元）．若每一件商品售价为
    lnx
    x
    （万元），通过市场分析，该厂生产的商品能全部售完．
    （1）写出年利润L（x）（万元）关于x的函数解析式；
    （2）年产量为多少件时，该厂在这一商品的生产中所获利润最大？

    查看答案和解析>>

    科目： 来源： 题型：

    已知点P（1+cosα，1-sinα），参数α∈R，点Q在曲线C：ρ=
    6
    		2
    sin(θ+
    π
    4
    )
    上．
    （1）求点P的轨迹方程和曲线C的直角坐标方程；
    （2）求点P与点Q之间距离的最大值．

    查看答案和解析>>

    科目： 来源： 题型：

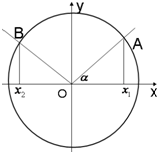    已知角α的始边与x轴的非负半轴重合，终边与单位圆O交于点A（x1，y1），将射线OA按逆时针方向旋转
    2π
    3
    后与单位圆O交于点B（x2，y2），f（α）=x1-x2；
    （Ⅰ）若角α为锐角，求f（α）的取值范围；
    （Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，若f（A）=
    3
    2
    ，c=3，△ABC的面积为3
    		3
    ，求a的值．

    查看答案和解析>>

    科目： 来源： 题型：

    空气质量指数（AQI）是衡量空气质量好坏的标准，表是我国南方某市气象环保部门从去年的每天空气质量检测数据中，随机抽取的40天的统计结果：
    空气质量指数（AQI）国家环保标准频数（天）频率
    [0，50]一级（优）4
    （50，100]二级（良）20
    （100，150]三级（轻度污染）8
    （150，200]四级（中度污染）4
    （200，300]五级（重度污染）3
    （300，+∞）六级（严重污染）1
    （1）若以这40天的统计数据来估计，一年中（365天）该市有多天的空气质量达到优良？
    （2）若将频率视为概率，某中学拟在今年五月份某三天召开运动会，以上表的数据为依据，问：
    ①这三天空气质量都达标（空气质量属一、二、三级内）的概率；
    ②这三天恰好有一天空气质量不达标（指四、五、六级）的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f（x）=
    2x
    x+1
    ，数列{an}的首项a1=
    2
    3
    ，且满足an+1=f（an），（n∈N*）
    （Ⅰ）令bn=
    1
    an
    -1，求证：数列{bn}是等比数列；
    （Ⅱ）令cn=
    n
    an
    ，求数列{cn}前n项和Sn．

    查看答案和解析>>

    科目： 来源： 题型：

    一盒中装有大小质地相同的小球，其中红球4个，白球、黑球各3个，
    （Ⅰ）从中任取两球，求取得的两球颜色不同的概率；
    （Ⅱ）将红球标上0，1，2，3；白球、黑球分别标上0，1，2；现从盒中任意取出两个小球．记所取出的两球标号之积为ξ，求ξ的分布列与数学期望．

    查看答案和解析>>

    同步练习册答案