练习册

  • 练习册
  • 试题
    相关习题
     0  211181  211189  211195  211199  211205  211207  211211  211217  211219  211225  211231  211235  211237  211241  211247  211249  211255  211259  211261  211265  211267  211271  211273  211275  211276  211277  211279  211280  211281  211283  211285  211289  211291  211295  211297  211301  211307  211309  211315  211319  211321  211325  211331  211337  211339  211345  211349  211351  211357  211361  211367  211375  266669 

    科目： 来源： 题型：

    如图所示，四边形PDCE为矩形，四边形ABCD为直角梯形，且∠BAD=∠ADC=90°，平面PDCE⊥平面ABCD，AB=AD=
    1
    2
    CD=1，PD=
    		2
    ．
    （Ⅰ）若M为PA中点，求证：AC∥平面MDE；
    （Ⅱ）求该几何体被平面PBD所分成的两部分的体积比．

    查看答案和解析>>

    科目： 来源： 题型：

    △ABC的内角A，B，C所对的边分别为a，b，c，向量
    m
    =（2sin
    B
    2
    ，2
    		2
    ），
    n
    =（cosB，2cos2
    B
    4
    -1），且
    m
    ∥
    n
    ．
    （Ⅰ）求角B的余弦值；
    （Ⅱ）若b=2，求S△ABC的最大值．

    查看答案和解析>>

    科目： 来源： 题型：

    网络公司为了解某地区人群上网情况，随机抽取了100名网民进行调查，其中女性有55名．下面是根据调查结果绘制的日均上网时间的频率分布图（时间单位为：时）：
    分组 [0，1） [1，2） [2，3） [3，4） [4，5） [5，6）
    频率  0.1 0.18  0.22   0.25 0.2   0.05
    将日均上网时间不低于4小时的网民成为“网迷”，已知“网迷”中有10名女性．
    （Ⅰ）根据已知条件完成下面2×2列联表，并判断是否有95%的把握认为“网迷”与性别有关？
      非网迷 网迷 合计
    男      
    女      
    合计      
    （Ⅱ）将日均上网时间不低于5小时的网民成为“超级网迷”，已知超级网迷中有2名女性，若从“超级网迷”中任意选取2人，求至少有1名女性网民的概率．
    附：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)

    P（K2≥k0）  0.100 0.050  0.010   0.001
     k0  2.706 3.841  6.635  10.828 

    查看答案和解析>>

    科目： 来源： 题型：

    已知a、b、c均为正实数，且a+b+c=1，求
    		a+1
    +
    		b+1
    +
    		c+1
    的最大值．

    查看答案和解析>>

    科目： 来源： 题型：

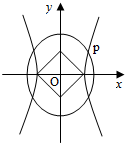    如图，O为坐标原点，双曲线C1：
    x2
    a
    2
    1
    -
    y2
    b
    2
    1
    =1（a1＞0，b1＞0）和椭圆C2：
    y2
    a
    2
    2
    +
    x2
    b
    2
    2
    =1（a2＞b2＞0）均过点P（
    2
    		3
    3
    ，1），且以C1的两个顶点和C2的两个焦点为顶点的四边形是面积为2的正方形．
    （Ⅰ）求C1、C2的方程；
    （Ⅱ）是否存在直线l，使得l与C1交于A、B两点，与C2只有一个公共点，且|
    OA
    +
    OB
    |=|
    AB
    |？证明你的结论．

    查看答案和解析>>

    科目： 来源： 题型：

    已知q和n均为给定的大于1的自然数，设集合M={0，1，2，…，q-1}，集合A={x|x=x1+x2q+…+xnqn-1，xi∈M，i=1，2，…n}．
    （Ⅰ）当q=2，n=3时，用列举法表示集合A；
    （Ⅱ）设s，t∈A，s=a1+a2q+…+anqn-1，t=b1+b2q+…+bnqn-1，其中ai，bi∈M，i=1，2，…，n．证明：若an＜bn，则s＜t．

    查看答案和解析>>

    科目： 来源： 题型：

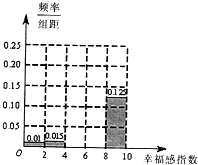    “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时，给出的区间内的一个数，该数越接近10表示越满意，为了解某大城市市民的幸福感，随机对该城市的男、女各500人市民进行了调查，调查数据如下表所示：
    幸福感指数[0，2）[2，4）[4，6）[6，8）[8，10）
    男市民人数1020220125125
    女市民人数1010180175125
    根据表格，解答下面的问题：
    （Ⅰ）完成频率分布直方图，并根据频率分布直方图估算该城市市民幸福感指数的平均值；（参考数据：2×1+3×3+40×5+30×7+25×9=646）
    （Ⅱ）如果市民幸福感指数达到6，则认为他幸福．试在犯错误概率不超过0.01的前提下能否判定该市市民幸福与否与性别有关？参考公式：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)

    P（K2≥k0）0.100.010.001
    k02.7066.63510.828

    查看答案和解析>>

    科目： 来源： 题型：

    已知数列{an}为等比数列，其前n项和为Sn，且满足16（a1+a4）+7=0，S1，S3，S2成等差数列．
    （1）求数列{an}的通项公式；
    （2）已知bn=n（n∈N+），记cn=（-1）nbnan-1，求数列{cn}前n项和f（n）．

    查看答案和解析>>

    科目： 来源： 题型：

    已知实数a＞0，函数f（x）=ex-ax-1（e为自然对数的底数）．
    （Ⅰ）求函数f（x）的单调区间及最小值；
    （Ⅱ）若f（x）≥0对任意的x∈R恒成立，求实数a的值．

    查看答案和解析>>

    科目： 来源： 题型：

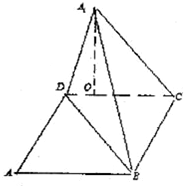    如图，矩形ABCD中，AB=10，BC=6，沿对角线BD吧△ABD折起到△A1BD的位置，使A1在平面BCD上的射影O恰好在CD上．
    （1）求证：BC⊥A1D；
    （2）求直线A1C与平面A1BD所成角的余弦值．

    查看答案和解析>>

    同步练习册答案