已知2f（x）+f（-x）=3x+2，求函数f（x）的解析式．

某同学完成一项任务共用去9h，他记录的完成工作量的百分数如下表：

时间/h	1	2	3	4	5	6	7	8	9
完成的百分数/%	15	30	45	60	60	70	80	90	100

（1）如果用T（x）表示x（h）后他完成工作量的百分数，那么T（5）是多少？求出T（x），并画出其图象；
（2）如果该同学在早晨8时开始工作，什么时候他在休息？

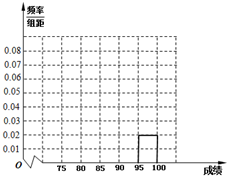某高中毕业学年，在高校自主招生期间，把学生的平时成绩按“百分制”折算，排出前n名学生，并对这n名学生按成绩分组，第一组[75，80），第二组[80，85），第三组[85，90），第四组[90，95），第五组[95，100]，如图为频率分布直方图的一部分，其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列，且第四组的人数为60．
（Ⅰ）请在图中补全频率分布直方图；
（Ⅱ）若Q大学决定在成绩高的第3，4，5组中用分层抽样的方法抽取6名学生进行面试．
①若Q大学本次面试中有B、C、D三位考官，规定获得两位考官的认可即面试成功，且面试结果相互独立，已知甲同学已经被抽中，并且通过这三位考官面试的概率依次为

1

2

、

1

3

，

1

5

，求甲同学面试成功的概率；
②若Q大学决定在这6名学生中随机抽取3名学生接受考官B的面试，第3组中有ξ名学生被考官B面试，求ξ的分布列和数学期望．

已知△ABC的三个内角A，B，C所对的边分别为a，b，c，且满足（b-a）（sinB+sinA）=（b-c）sinC，cosC=

3

3

，a=3．
（Ⅰ）求sinB；
（Ⅱ）求△ABC的面积．

己知函数f（x）=lnx-e^x+a
（I）若x=1是，f（x）的极值点，讨论f（x）的单调性
（Ⅱ）当a≥-2时，证明：f（x）＜0．

已知函数f（x）=x⁴+x²-1，g（x）=ax³+x²+b（x∈R），其中a，b∈R．
（Ⅰ）若曲线y=f（x）与y=g（x）在点（1，1）处相交且有相同的切线，求a，b的值；
（Ⅱ）设F（x）=f（x）+g（x），若对于任意的a∈[-2，2]，函数y=F（x）在区间[-1，1]上的值恒为负数，求b的取值范围．

已知函数f（x）=lnx+

a

x+1

．
（1）当a=2时，证明对任意的x∈（1，+∞），f（x）＞1；
（2）求证：ln（n+1）＞

1

3

+

1

5

+

1

7

+…+

1

2n+1

（n∈N^*）．
（3）若函数f（x）有且只有一个零点，求实数a的取值范围．

生产A，B两种元件，其质量按测试指标划分为：指标大于或等于82为正品，小于82为次品，现随机抽取这两种元件各100件进行检测，检测结果统计如下：

测试指标	[70，76）	[76，82）	[82，88）	[88，94）	[94，100]
元件A	8	12	40	32	8
元件B	7	18	40	29	6

（Ⅰ）试分别估计元件A、元件B为正品的概率；
（Ⅱ）生产一件元件A，若是正品可盈利50元，若是次品则亏损10元；生产一件元件B，若是正品可盈利100元，若是次品则亏损20元，在（Ⅰ）的前提下：
（i）求生产5件元件B所获得的利润不少于300元的概率；
（ii）记X为生产1件元件A和1件元件B所得的总利润，求随机变量X的分布列和数学期望．

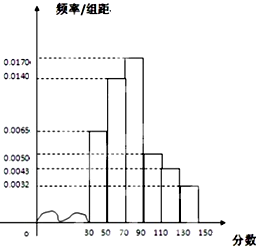衡水市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰．若现有500人参加测试，学生成绩的频率分布直方图如图：
（Ⅰ）求获得参赛资格的人数；
（Ⅱ）根据频率直方图，估算这500名学生测试的平均成绩；
（Ⅲ）若知识竞赛分初赛和复赛，在初赛中每人最多有5次选题答题的机会，累计答对3题或答错3题即终止，答对3题者方可参加复赛，已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为

1

9

，求甲在初赛中答题个数的分布列及数学期望．

f（x）定义域为（0，+∞），且满足f（x）-2x•f（

1

x

）+3x²=0，求f（x）=？