
科目: 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
已知10件不同的产品中共有3件次品,现对它们进行一一测试,直到找出所有3件次品为止.
(1)求恰好在第5次测试时3件次品全部被测出的概率;
(2)记恰好在第k次测试时3件次品全部被测出的概率为f(k),求f(k)的最大值和最小值.
查看答案和解析>>
科目: 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子任取2个球,乙从箱子里在取1个球,若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的数学期望.
查看答案和解析>>
科目: 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
某热水瓶胆生产的6件产品中,有4件正品,2件次品,正品和次品在外观上没有区别,从这6件产品中任意抽检2件,计算
(1)2件都是正品的概率
(2)至少有一件次品的概率.
查看答案和解析>>
科目: 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
袋子A和袋子B均装有红球和白球,从A中摸出一个红球的概率是 ,从B中摸出一个红球的概率是P.
,从B中摸出一个红球的概率是P.
(1)从A中有放回地摸球,每次摸出一个,共摸5次,求恰好有3次摸到红球的概率;
(2)若A、B两个袋子中的总球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率为 ,求P的值.
,求P的值.
查看答案和解析>>
科目: 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
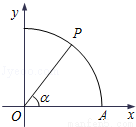
(Ⅰ)若点P的坐标是(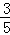 ,
, ),求cos2
),求cos2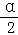 ﹣sin2
﹣sin2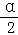 +2sin
+2sin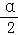 cos
cos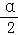 的值;
的值;
(Ⅱ)求函数f(α)=sinα+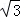 cosα的值域.
cosα的值域.
查看答案和解析>>
科目: 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
某批产品共10件,已知从该批产品中任取1件,则取到的是次品的概率为P=0.2.若从该批产品中任意抽取3件,
(1)求取出的3件产品中恰好有一件次品的概率;
(2)求取出的3件产品中次品的件数X的概率分布列与期望.
查看答案和解析>>
科目: 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
某校高二年级某班的数学课外活动小组有6名男生,4名女生,从中选出4人参加数学竞赛考试,用X表示其中男生的人数,
(1)请列出X的分布列;
(2)根据你所列的分布列求选出的4人中至少有3名男生的概率.
查看答案和解析>>
科目: 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
生产方提供50箱的一批产品,其中有2箱不合格产品.采购方接收该批产品的准则是:从该批产品中任取5箱产品进行检测,若至多有1箱不合格产品,便接收该批产品.问:该批产品被接收的概率是多少?
查看答案和解析>>
科目: 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
某班组织知识竞赛,已知题目共有10道,随机抽取3道让某人回答,规定至少要答对其中2道才能通过初试,他只能答对其中6道,试求:
(1)抽到他能答对题目数的分布列;
(2)他能通过初试的概率.
查看答案和解析>>
科目: 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
(2011•遂宁二模)点P在直径为 的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )
的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )
A. B.6 C.
B.6 C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com