
科目: 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:填空题
已知定义在R上的奇函数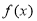 ,当
,当 时,
时,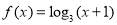 .若关于
.若关于 的不等式
的不等式 的解集为
的解集为 ,函数
,函数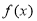 在
在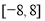 上的值域为
上的值域为 ,若“
,若“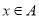 ”是“
”是“ ”的充分不必要条件,则实数
”的充分不必要条件,则实数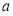 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:填空题
已知曲线 :
: 在点
在点
 (
( )处的切线
)处的切线 的斜率为
的斜率为 ,直线
,直线 交
交 轴,
轴, 轴分别于点
轴分别于点 ,
, ,且
,且 .给出以下结论:
.给出以下结论:
① ;
;
②当 时,
时, 的最小值为
的最小值为 ;
;
③当 时,
时, ;
;
④当 时,记数列
时,记数列 的前
的前 项和为
项和为 ,则
,则 .
.
其中,正确的结论有 (写出所有正确结论的序号)
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:解答题
(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球.现从中同时取出3个球.
(Ⅰ)求恰有一个黑球的概率;
(Ⅱ)记取出红球的个数为随机变量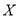 ,求
,求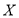 的分布列和数学期望
的分布列和数学期望 .
.
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图, 为正三角形,
为正三角形, 平面
平面 ,
, ,
, 为
为 的中点,
的中点, ,
, .
.

(Ⅰ)求证:
 平面
平面 ;
;
(Ⅱ)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知数列 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 满足
满足 ,
, .
. .
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)记 ,
, .求数列
.求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:解答题
(本小题满分12分)某大型企业一天中不同时刻的用电量 (单位:万千瓦时)关于时间
(单位:万千瓦时)关于时间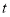 (
(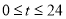 ,单位:小时)的函数
,单位:小时)的函数 近似地满足
近似地满足 ,下图是该企业一天中在0点至12点时间段用电量
,下图是该企业一天中在0点至12点时间段用电量 与时间
与时间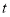 的大致图象.
的大致图象.
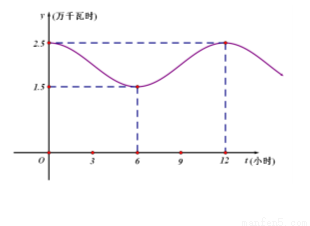
(Ⅰ)根据图象,求 ,
, ,
, ,
, 的值;
的值;
(Ⅱ)若某日的供电量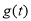 (万千瓦时)与时间
(万千瓦时)与时间 (小时)近似满足函数关系式
(小时)近似满足函数关系式 (
(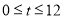 ).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1).
).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1).
参考数据:
| 10 | 11 | 12 | 11.5 | 11.25 | 11.75 | 11.625 | 11.6875 |
| 2.25 | 2.433 | 2.5 | 2.48 | 2.462 | 2.496 | 2.490 | 2.493 |
| 5 | 3.5 | 2 | 2.75 | 3. 125 | 2.375 | 2.563 | 2.469 |
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知椭圆 :
: (
( )的右焦点为
)的右焦点为 ,且椭圆
,且椭圆 上一点
上一点 到其两焦点
到其两焦点 的距离之和为
的距离之和为 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设直线 与椭圆
与椭圆 交于不同两点
交于不同两点 ,
, ,且
,且 .若点
.若点 满足
满足 ,求
,求 的值.
的值.
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数 ,
, ,其中
,其中 且
且 .
.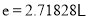 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当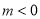 时,求函数
时,求函数 的单调区间和极小值;
的单调区间和极小值;
(Ⅱ)当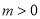 时,若函数
时,若函数 存在
存在 三个零点,且
三个零点,且 ,试证明:
,试证明:
 ;
;
(Ⅲ)是否存在负数 ,对
,对 ,
, ,都有
,都有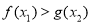 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷(解析版) 题型:选择题
若一个几何体的正视图和侧视图是两个全等的正方形,则这个几何体的俯视图不可能是( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com