
科目: 来源: 题型:
设数列{an}的首项a1=a≠ ,且
,且
an+1=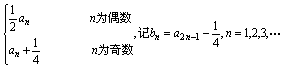
(Ⅰ)求a2,a3;
(Ⅱ)判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)求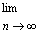 (b1+b2+b3+…+bn).
(b1+b2+b3+…+bn).
查看答案和解析>>
科目: 来源: 题型:
已知数列{an}的各项都是正数,且满足:a0=1,an+1= an·(4-an),n
an·(4-an),n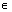 N.
N.
(1)证明an<an+1<2,n∈N.
(2)求数列{an}的通项公式an.
查看答案和解析>>
科目: 来源: 题型:
设无穷等差数列{an}的前n项和为Sn.
(Ⅰ)若首项a1=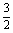 ,公差d=1,求满足Sk2=(Sk)2的正整数k;
,公差d=1,求满足Sk2=(Sk)2的正整数k;
(Ⅱ)求所有的无穷等差数列{an};使得对于一切正整数中k都有Sk2=(Sk)2成立.
查看答案和解析>>
科目: 来源: 题型:
等差数列{an}中,a1+a2+a3=-24,a18+a19+ a20=78,则此数列前20项和等于 ( )
a20=78,则此数列前20项和等于 ( )
A.160 B.180 C. 200 D.220
查看答案和解析>>
科目: 来源: 题型:
设f(x)=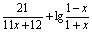 (-1<x<1).
(-1<x<1).
(1)求证:该函数在其定义域内是减函数.
(2)设h(x)=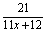 解方程f(x)-h(x)=-1.
解方程f(x)-h(x)=-1.
如果函数g(x)=lg(ax2+2f-1(0)x+1)的值域为全体实数,试求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
校食堂改建一个开水房,计划用电炉或煤炭烧水,但用煤时也要用电鼓风及时排气,用煤烧开水每吨开水费用S元,用电炉烧开水每吨开水费用为P元,S=5m+0.8n+5,P=10.8n+20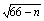 .其中m为每吨煤的价格,n为每百度电的价格;如果烧煤时的费用不超过用电炉时的费用,则用煤烧水;否则就用电炉烧水.
.其中m为每吨煤的价格,n为每百度电的价格;如果烧煤时的费用不超过用电炉时的费用,则用煤烧水;否则就用电炉烧水.
(1)如果两种方法烧水费用相同,试将每吨煤的价格表示为每百度电价的函数;

(2)已知现在每百度电价不低于50元,那么当每吨煤的最高价不超过多少元时可以选择 用煤?
用煤?
查看答案和解析>>
科目: 来源: 题型:
已知f(x)=ax2+bx+c,其中a∈N,b,c∈Z.
(1)若b>2a,在[-1,1]上是否存在x使得|f(x|>b成立.
(2)当方程f(x)-x=0的根在(0,1)内时,试求a的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com