
科目: 来源: 题型:
甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格。
(1)分别求甲、乙两人考试 合格的概率;
合格的概率;
(2)求甲、乙两人至少有一人考试合格的概率。
查看答案和解析>>
科目: 来源: 题型:
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.

(1)求证:AM⊥PD;
(2)求直线CD与平面ACM所成的角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
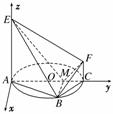
(1)证明:EM⊥BF;
(2)求平面BEF与平面ABC所成的锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
四棱锥P-ABCD中,底面ABCD是一个平行四边形,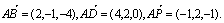
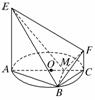 (1)求证:PA⊥底面ABCD;
(1)求证:PA⊥底面ABCD;
(2)求四棱锥P-ABCD的体积;
(3)对于向量a=(x1,y1,z1).b=(x2,y2,z2),c=(x3,y3,z3 )定义一种运算:
)定义一种运算:
(a×b)·c=x1y2z3+x2y3z1+x3y1z2-x1y3z2-x2y1z3-x3y2z1试计算(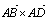 )
)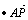 的绝对值的值;说明其与四棱锥P-ABCD体积的关系,并同此猜想这一运算(
的绝对值的值;说明其与四棱锥P-ABCD体积的关系,并同此猜想这一运算(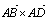 )
)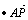 的绝对值的几何意义。
的绝对值的几何意义。
查看答案和解析>>
科目: 来源: 题型:
在三棱柱ABC-A1B1C1中,A1在底面上的射影在线段AC上,底面△ABC是以∠B为直角的等腰三角形,M为AC的中点,又AB=AA1=a
(1)求证:BM⊥AA1;
(2)若A1C⊥平面BMC1,求证:三棱柱ABC-A1B1C1为直三棱柱。
查看答案和解析>>
科目: 来源: 题型:
四棱锥P=ABCD中,AB⊥CD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。
(1)求证BM∥平面PAD;
(2)在△PAD内找一点N,使MN⊥平面PBD;
(3)求直线PC与平面PBD所成角的正弦值。
查看答案和解析>>
科目: 来源: 题型:
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,BC=AC=2,AA1=4,D为棱CC1上的一动点,M、N分别为△ABD、△A1B1D的重心。
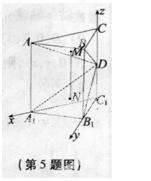
(1)求证:MN⊥BC;
(2)若二面角C-AB-D的大小 为arctan
为arctan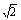 ,求点C1到平面A1B1D的距离;
,求点C1到平面A1B1D的距离;
(3)若点C在△ABD上的射影正好为M,试判断点C1在△A1B1D的射影是否为N?并说明理由。
查看答案和解析>>
科目: 来源: 题型:
直三棱柱ABC-A′B′C′中,AC=BC=AA′,∠ACB=90°,D、E分别为AB、BB′的中点.
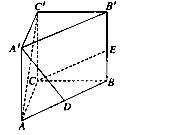
(1)求证:CE⊥A′D;
(2)求异面直线CE与AC′所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com