
科目: 来源: 题型:
已知圆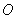 的方程为
的方程为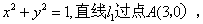 且与圆
且与圆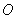 相切.
相切.
(Ⅰ)求直线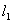 的方程;
的方程;
(Ⅱ)设圆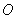 与
与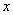 轴交于
轴交于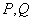 两点,M是圆
两点,M是圆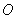 上异于
上异于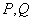 的任意一点,过点
的任意一点,过点 且与
且与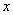 轴垂直的直线为
轴垂直的直线为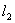 ,直线
,直线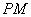 交直线
交直线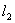 于点
于点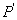 ,直线
,直线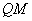 交直线
交直线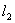 于点
于点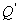 .
.
求证:以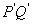 为直径的圆
为直径的圆 总过定点,并求出定点坐标.
总过定点,并求出定点坐标.
查看答案和解析>>
科目: 来源: 题型:
在平面直角坐标系 中,点
中,点 ,直线
,直线 经过两点
经过两点 ,
, ,设圆
,设圆 的半径为
的半径为 ,圆心在直线
,圆心在直线 上.
上.
(Ⅰ)求直线 的方程;
的方程;
(Ⅱ) 若圆 被
被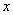 轴截得的弦长为
轴截得的弦长为 ,求圆
,求圆 的方程;
的方程;
(Ⅲ) 若圆 上存在点
上存在点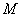 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100) | 2 | 0.1 |
| 合计 | 20 | 1 |
(Ⅰ) 根据上面的频率分布表,估计该居民区PM2.5的24小时平均浓度超过50微克/立方米的概率;
(Ⅱ)计算样本众数、中位数和平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
查看答案和解析>>
科目: 来源: 题型:
某同学大学毕业后在一家公司上班,工作年限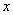 和年收入
和年收入 (万元),有以下的统计数据:
(万元),有以下的统计数据:
|
| 3 | 4 | 5 | 6 |
|
| 2.5 | 3 | 4 | 4.5 |
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)根据上表提供的数据,用最小二乘法求得 关于
关于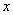 的线性回归方程为
的线性回归方程为
求 的值;
的值;
(Ⅲ)请你估计该同学第8年的年收入约是多少?
查看答案和解析>>
科目: 来源: 题型:
将一枚质地均匀且四个面上分别标有1,2,3,4的正四面体先后抛掷两次,其底面落于桌面上,记第一次朝下面的数字为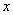 ,第二次朝下面的数字为
,第二次朝下面的数字为 。用
。用 表示一个基本事件。
表示一个基本事件。
(Ⅰ).请写出所有的基本事件;
(Ⅱ).求满足条件“ 为整数”的事件的概率;
为整数”的事件的概率;
(Ⅲ).求满足条件“ ”的事件的概率。
”的事件的概率。
查看答案和解析>>
科目: 来源: 题型:
设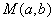 ,且满足
,且满足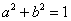 ,已知圆
,已知圆 ,
,
直线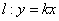 ,下列四个命题:
,下列四个命题:
①对满足条件的任意点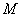 和任意实数
和任意实数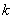 ,直线
,直线 和圆
和圆 有公共点;
有公共点;
②对满足条件的任意点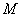 和任意实数
和任意实数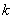 ,直线
,直线 和圆
和圆 相切;
相切;
③对任意实数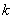 ,必存在满足条件的点
,必存在满足条件的点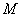 ,使得直线
,使得直线 和圆
和圆 相切;
相切;
④对满足条件的任意点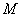 ,必存在实数
,必存在实数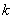 ,使得直线
,使得直线 和圆
和圆 相切.
相切.
其中正确的命题是 .(写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com