
科目: 来源: 题型:
设{an}是公比不为1的等比数列,其前n项和为Sn,且a5,a3,a4成等差数列.
(1) 求数列{an}的公比;
(2) 证明:对任意k∈N+,Sk+2,Sk,Sk+1成等差数列.
查看答案和解析>>
科目: 来源: 题型:
已知数列{an}是首项为1,公差为d的等差数列,数列{bn}是首项为1,公比为q(q>1)的等比数列.
(1) 若a5=b5,q=3,求数列{an·bn}的前n项和;
(2) 若存在正整数k(k≥2),使得ak=bk.试比较an与bn的大小,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
已知等差数列{an}满足:an+1>an(n∈N*),a1=1,该数列的前三项分别加上1,1,3后顺次成为等比数列{bn}的前三项.
(1) 分别求数列{an}、{bn}的通项公式;
(2) 设Tn=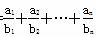 (n∈N*),若Tn+
(n∈N*),若Tn+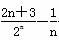 <c(c∈Z)恒成立,求c的最小值.
<c(c∈Z)恒成立,求c的最小值.
查看答案和解析>>
科目: 来源: 题型:
已知各项均为正数的等比数列{an}的公比为q,且0<q<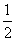 .
.
(1) 在数列{an}中是否存在三项,使其成等差数列?说明理由;
(2) 若a1=1,且对任意正整数k,ak-(ak+1+ak+2)仍是该数列中的某一项.
(ⅰ) 求公比q;
(ⅱ) 若bn=-logan+1(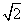 +1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2 011表示T2 011.
+1),Sn=b1+b2+…+bn,Tr=S1+S2+…+Sn,试用S2 011表示T2 011.
查看答案和解析>>
科目: 来源: 题型:
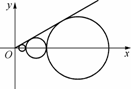
设C1、C2、…、Cn、…是坐标平面上的一列圆,它们的圆心都在轴的正半轴上,且都与直线y= x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
x相切,对每一个正整数n,圆Cn都与圆Cn+1相互外切,以rn表示Cn的半径,已知{rn}为递增数列.
(1) 证明:{rn}为等比数列;
(2) 设r1=1,求数列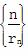 的前n项和.
的前n项和.
查看答案和解析>>
科目: 来源: 题型:
水土流失是我国西部大开发中最突出的问题,全国9 100万亩坡度为25°以上的坡耕地需退耕还林,其中西部占70%,2002年国家确定在西部地区退耕还林面积为515万亩,以后每年退耕土地面积递增12%.
(1) 试问,从2002年起到哪一年西部地区基本上解决退耕还林问题?
(2) 为支持退耕还林工作,国家财政补助农民每亩300斤粮食,每斤粮食按0.7元计算,并且每亩退耕地每年补助20元,试问到西部地区基本解决退耕还林问题时,国家财政共需支付约多少亿元?
查看答案和解析>>
科目: 来源: 题型:
某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1) 求该企业使用该设备x年的年平均污水处理费用y(万元);
(2) 为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com