
科目: 来源: 题型:
已知 椭圆C:
椭圆C: (a>b>0)上任一点P到两个焦点的距离的和为2
(a>b>0)上任一点P到两个焦点的距离的和为2 ,P与椭圆长轴两顶点连线的斜率之积为-
,P与椭圆长轴两顶点连线的斜率之积为- .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
(1)若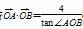 (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值;
(2)当直线l与两坐标轴都不垂直时,在x轴上是否总存在点Q,使得直线QA,QB的倾斜角互为补角?若存在,求出点Q坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
某创业投资公司 拟投资开发某种新能源
拟投资开发某种新能源 产品,估计能获得10万元到1 000万元的投资收益.现准备制定一个对科研课题组的奖励方案:资金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
产品,估计能获得10万元到1 000万元的投资收益.现准备制定一个对科研课题组的奖励方案:资金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)若建立函数y=f(x)模型制定奖励方案,试用数学语言表述该公司对奖励函数f(x)模型的基本要求,并分析函数y=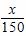 +2是否符合公司要求的奖励函数模型,并说明原因;
+2是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用模型函数y=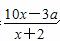 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.
查看答案和解析>>
科目: 来源: 题型:
如图,在四棱锥P ABCD中,PA⊥底面ABCD,AC⊥CD,∠DAC=60°,AB=BC=AC,E是PD的中点,F为ED的中点.
(1)求证:平面PAC⊥平面PCD;
(2)求证:CF∥平面BAE.

查看答案和解析>>
科目: 来源: 题型:
已知向量m=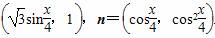 (1)若m·n=1,求cos
(1)若m·n=1,求cos 的值;
的值;
(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a, b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
查看答案和解析>>
科目: 来源: 题型:
已知无穷数列{an}的各项均为正整数,Sn为数列{an}的前n项和.
(1)若数列{an}是等差数列,且对任意正整数n都有Sn3=(Sn)3成立,求数列{an}的通项公式;
(2)对任意正整数n,从集合{a1,a2,…,an}中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与a1,a2,…,an一起恰好是1至Sn全体正整数组成的集合.
(ⅰ)求a1,a2的值;
(ⅱ)求 数列{an}的通项公式.
数列{an}的通项公式.
查看答案和解析>>
科目: 来源: 题型:
已知函数f(x)=aln x= (a为常数
(a为常数 ).
).
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-5=0垂直,求a的值;
(2)求函数f(x)的单调区间;
(3)当x≥1时,f(x)≤2x-3恒成立,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1: =1,A1,A2分别为椭圆C1的左、右顶点.椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”.
=1,A1,A2分别为椭圆C1的左、右顶点.椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”.
(1)求椭圆C2的方程;
(2)设P为椭圆C2上异于A1,A2的任意一点,过P作PQ⊥x轴,垂足为Q,线段PQ交椭圆C1于点H.求证:H为△PA1A2的垂心.(垂心为三角形三条高的交点)

查看答案和解析>>
科目: 来源: 题型:
如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池 ,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的PQRS面积为S2.
,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的PQRS面积为S2.
(1)用a,θ表示S1和S2;
(2)当a固定,θ变化时,求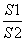 的最小值.
的最小值.

查看答案和解析>>
科目: 来源: 题型:
在等腰梯形ABCD中,AB∥CD,AB=BC=AD= 2,CD=4,E为边DC的中点,如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
2,CD=4,E为边DC的中点,如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
(1)若PA∥平面MQB,求PM∶MC;
(2)若平面AEP⊥平面ABCE,点M是PC的中点,求三棱锥A MQB的体积.
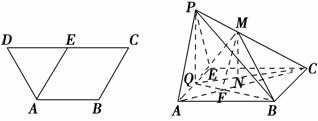
图1 图2
查看答案和解析>>
科目: 来源: 题型:
已知△ABC中,角A,B,C的对边分别为a,b,c,且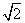 acos B=ccos B+bcos C.
acos B=ccos B+bcos C.
(1)求角B的大小;
(2)设向量m=(cos A,cos 2A),n=(12,-5),求当m·n取最大值时,tan C的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com