
科目: 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:填空题
若曲线y=ax+lnx在点(1,a)处的切线方程为y=2x+b,则b= _________ .
查看答案和解析>>
科目: 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:填空题
设△ABC的内角A,B,C的对边分别为a,b,c,且a=1,b= ,cosC=﹣
,cosC=﹣ ,则sinB= _________ .
,则sinB= _________ .
查看答案和解析>>
科目: 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:填空题
已知点P(x,y)的坐标满足 ,则z=x+2y的最大值为 _________ .
,则z=x+2y的最大值为 _________ .
查看答案和解析>>
科目: 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:填空题
若函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是单调增函数,如果实数t满足f(t)+f(﹣t)<2f(1),那么t的取值范围是 _________ .
查看答案和解析>>
科目: 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:解答题
(12分)设数列{an}是公比为正数的等比数列,a1=2,a3﹣a2=12.
(1)求数列{an}的通项公式;
(2)设数列{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目: 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:解答题
(12分)如图,四边形ABCD为矩形,四边形ADEF为梯形,FE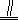
 AD,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=2,点G为AC的中点.
AD,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=2,点G为AC的中点.
(Ⅰ)求证:EG∥平面ABF;
(Ⅱ)求三棱锥B﹣AEG的体积.
查看答案和解析>>
科目: 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:解答题
(12分)某市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由于空气污染造成的经济损失为S(单位:元),空气质量指数API为ω,在区间[0,100]对企业没有造成经济损失;在区间(100,300]对企业造成经济损失成直线模型(当API为150时造成的经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的经济损失为2000元.
(1)试写出S(ω)表达式;
(2)试估计在本年内随机抽取一天,该天经济损失S大于500元且不超过900元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
P(K2≥kc) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
Kc | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2=
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
查看答案和解析>>
科目: 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:解答题
(12分)如图,已知椭圆 的右顶点为A(2,0),点P(2e,
的右顶点为A(2,0),点P(2e, )在椭圆上(e为椭圆的离心率).
)在椭圆上(e为椭圆的离心率).

(1)求椭圆的方程;
(2)若点B,C(C在第一象限)都在椭圆上,满足 ,且
,且 ,求实数λ的值.
,求实数λ的值.
查看答案和解析>>
科目: 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:解答题
(12分)已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,(a为常数,e为自然对数的底,e≈2.71828).
(1)当a=1时,求f(x)的单调区间;
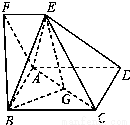
(2)若f(x)>0在区间(0,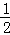 )上恒成立,求a的最小值.
)上恒成立,求a的最小值.
查看答案和解析>>
科目: 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:解答题
(10分)如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,连接AC,过点A作AD⊥CD于点D,交⊙O于点E.
(Ⅰ)证明:∠AOC=2∠ACD;
(Ⅱ)证明:ABCD=ACCE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com