
科目: 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:填空题
设函数f(x)= (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))= , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))= , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))= ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
查看答案和解析>>
科目: 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:填空题
对于实数x,用[x]表示不超过x的最大整数,如[-0.5]=-1, [3, 2]=3,若n∈N*, an=[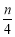 ], Sn为数列{an}的前n项和,则S8= ,S4n= .
], Sn为数列{an}的前n项和,则S8= ,S4n= .
查看答案和解析>>
科目: 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:填空题
设点P(x, y)为函数y=x2-2(x>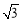 )图像上一动点,记m=
)图像上一动点,记m= , 则当m取最小值时,点P的坐标为 .
, 则当m取最小值时,点P的坐标为 .
查看答案和解析>>
科目: 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)设数列{an}的前n项和为Sn,对任意的正整数n,都有an=4Sn+1成立.
(1)求数列{an}的通项公式;
(2)设bn=log3|an|,数列{ }的前n项和为Tn, 求证:Tn<
}的前n项和为Tn, 求证:Tn< .
.
查看答案和解析>>
科目: 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)某校在一次对学生在课外活动中喜欢跑步和喜欢打球的学生的抽样调查中,随机抽取了100名同学,相关数据如下表所示:
喜欢跑步 | 喜欢打球 | 总计 | |
男生 | 23 | 32 | 55 |
女生 | 29 | 16 | 45 |
总计 | 52 | 48 | 100 |
(1)由表中数据直观分析,喜欢打球的学生是否与性别有关?
(2)用分层抽样的方法在喜欢打球的学生中随机抽取6名,男学生应该抽取几名?
(3)在上述抽取的6名学生中任取2名,求恰有1名女学生的概率.
查看答案和解析>>
科目: 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.

(1)求三棱锥P—ACD的外接球的表面积;
(2)若M为PB的中点,问在AD上是否存在一点E,使AM∥平面PCE?若存在,求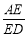 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)设椭圆C: 过点M(
过点M( ,
,  ),且离心率为
),且离心率为 ,直线l过点P(3, 0),且与椭圆C交于不同的A、B两点。
,直线l过点P(3, 0),且与椭圆C交于不同的A、B两点。
(1)求椭圆C的方程;
(2)求 ·
· 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)设函数f(x)=sinx, g(x)=ax,(a为常数),若f(x)≥g(x),对x∈[0, 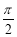 ]恒成立。
]恒成立。
(1)求a的最大值;
(2)对任意的锐角三角形ABC,均有sinA+sinB+sinC>M恒成立,求实数M的取值范围.
查看答案和解析>>
科目: 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—1:几何证明选讲
如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠BAC的平分线与BC和圆O分别交于点D和E.

(1)求证: ;
;
(2)求AD·AE的值.
查看答案和解析>>
科目: 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线l的参数方程为 (t为参数,m为常数),以直角坐标系xOy的原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为:ρ2-2ρsinθ-4=0,且直线l与圆C交于A、B两点.
(t为参数,m为常数),以直角坐标系xOy的原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为:ρ2-2ρsinθ-4=0,且直线l与圆C交于A、B两点.
(1)若|AB|= ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)若点P的极坐标为( ,
, ),且满足2
),且满足2 ,求此时直线l的直角坐标方程.
,求此时直线l的直角坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com