
科目: 来源: 题型:
有2n个数字,其中一半是奇数,一半是偶数,从中任取两个数,则所取的两数之和为偶数的概率是………………………………………………………( )
A、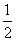 B、
B、 C、
C、 D、
D、
查看答案和解析>>
科目: 来源: 题型:
设口袋中有黑球、白球共7个,从中任取2个球,已知取到白球个数的数学期望值为 ,则口袋中白球的个数为 …………………………………… …( )
,则口袋中白球的个数为 …………………………………… …( )
A.3 B.4 C.5 D.2
查看答案和解析>>
科目: 来源: 题型:
如图,将一个四棱锥的每一个顶点染一种颜色,并使同一条棱上的两端点异色,如果只有4种颜色可供使用,则不同的染色方法有……………………( )
A.58种 B.60种 C.72种 D.84种
 |
查看答案和解析>>
科目: 来源: 题型:
已知三个正态分布密度函数φi(x)= e-
e- (x∈R,i=1,2,3)的图象如图所示,则…………………………………( )
(x∈R,i=1,2,3)的图象如图所示,则…………………………………( )
A.μ1<μ2=μ3,σ1=σ2>σ3
B.μ1>μ2=μ3,σ1=σ2<σ3
C.μ1=μ2<μ3,σ1<σ2=σ3
D.μ1<μ2=μ3,σ1=σ2<σ3
查看答案和解析>>
科目: 来源: 题型:
.如图,棱柱ABCD—A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.(1)求异面直线BD和AA1所成的角;(2)求二面角D—A1A—C的平面角的余弦值;(3)在直线CC1上否存在点P,使BP∥平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:
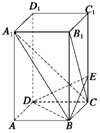
如图所示,已知长方体ABCD—A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C.(1)求CE的长;(2)求证:A1C⊥平面BED;(3)求A1B与平面BDE夹角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com