
科目: 来源: 题型:
设a=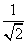 (sin56°-cos56°), b=cos50°·cos128°+cos40°·cos38°,
(sin56°-cos56°), b=cos50°·cos128°+cos40°·cos38°,
c=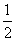 (cos80°-2cos250°+1),则a,b,c的大小关系是 ( )
(cos80°-2cos250°+1),则a,b,c的大小关系是 ( )
A.a>b>c B.b>a>c C.c>a>b D.a>c>b
查看答案和解析>>
科目: 来源: 题型:
已知e1,e2是夹角为60°的两个单位向量,若a=e1+e2,b=-4e1+2e2,则a与b的
夹角为 ( )
A.30° B.60° C.120° D.150°
查看答案和解析>>
科目: 来源: 题型:
在(1+x+x2)n=D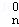 +D
+D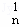 x+D
x+D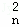 x2+…+D
x2+…+D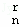 xr+…+D
xr+…+D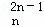 x2n﹣1+D
x2n﹣1+D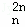 x2n的展开式中,把D
x2n的展开式中,把D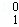 ,D
,D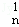 ,D
,D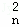 ,…,D
,…,D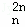 叫做三项式系数.
叫做三项式系数.
(1)当n=2时,写出三项式系数D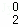 ,D
,D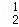 ,D
,D ,D
,D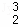 ,D
,D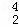 的值;
的值;
(2)类比二项式系数性质C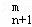 =C
=C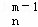 +C
+C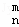 (1≤m≤n,m∈N,n∈N),给出一个关于三项式系数D
(1≤m≤n,m∈N,n∈N),给出一个关于三项式系数D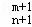 (1≤m≤2n﹣1,m∈N,n∈N)的相似性质,并予以证明;
(1≤m≤2n﹣1,m∈N,n∈N)的相似性质,并予以证明;
(3)求D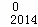 C
C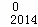 ﹣D
﹣D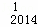 C
C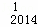 +D
+D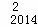 C
C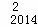 ﹣
﹣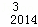 C
C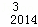 +…+D
+…+D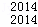 C
C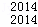 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
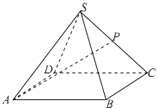
如图,已知正四棱锥S﹣ABCD的底面边长为2,高为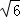 ,P为棱SC的中点.
,P为棱SC的中点.
(1)求直线AP与平面SBC所成角的正弦值;
(2)求两面角B﹣SC﹣D大小的余弦值;
(3)在正方形ABCD内是否有一点Q,使得PQ⊥平面SDC?若存在,求PQ的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
观察下列各不等式:
1+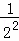 <,
<,
1+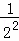 +
+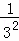 <,
<,
1+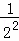 +
+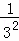 +
+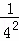 <,
<,
1+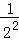 +
+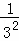 +
+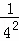 +
+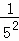 <,
<,
…
(1)由上述不等式,归纳出一个与正整数n(n≥2)有关的一般性结论;
(2)用数学归纳法证明你得到是结论.
查看答案和解析>>
科目: 来源: 题型:
某同学参加高二学业水平测试的4门必修科目考试.已知该同学每门学科考试成绩达到“A”等级的概率均为,且每门考试成绩的结果互不影响.
(1)求该同学至少得到两个“A”的概率;
(2)已知在高考成绩计分时,每有一科达到“A”,则高考成绩加1分,如果4门学科均达到“A”,则高考成绩额外再加1分.现用随机变量Y表示该同学学业水平测试的总加分,求Y的概率分别列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com