
科目: 来源: 题型:
某商场有来自三个国家的进口奶制品,其中A国、B国、C国的奶制品分别有40种、10种、30种,现从中抽取一个容量为16的样本进行三聚氰胺检测,若采用分层抽样的方法抽取样本,则抽取来自B国的奶制品________种.
查看答案和解析>>
科目: 来源: 题型:
某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系数抽样三种方案.使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有如下四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270.
关于上述样本的下列结论中,正确的是( )
A.②③都不能为系统抽样 B.②④都不能为分层抽样
C.①④都可能为系统抽样 D.①③都可能为分层抽样
查看答案和解析>>
科目: 来源: 题型:
当前,某城市正分批修建经济适用房以解决低收入家庭住房紧张问题.已知甲、乙、丙三个社区现分别有低收入家庭360户、270户、180户,若第一批经济适用房中有90套住房用于解决这三个社区中90户低收入家庭的住房问题,现采用分层抽样的方法决定各社区户数,则应从乙社区中抽取低收入家庭的户数为( )
A.40 B.36 C.30 D.20
查看答案和解析>>
科目: 来源: 题型:
某校要从高一、高二、高三共2 012名学生中选取50名组成志愿团,若采用下面的方法选取,先用简单随机抽样的方法从2 012人中剔除12人,剩下的2 000人再按分层抽样的方法进行,则每人入选的概率( )
A.都相等且为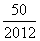 B.都相等且为
B.都相等且为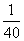
C.不会相等 D.均不相等
查看答案和解析>>
科目: 来源: 题型:
某班共有学生54人,学号分别为1~54号,现根据学生的学号,用系统抽样的方法,抽取一个容量为4的样本,已知3号、29号、42号的同学在样本中,那么样本中还有一个同学的学号是( )
A.10 B.16 C.53 D.32
查看答案和解析>>
科目: 来源: 题型:
某校高三一班有学生54人,二班有学生42人,现在要用分层抽样的方法从两个班抽出16人参加军训表演,则一班和二班分别被抽取的人数是( )
A.8,8 B.10,6 C.9,7 D.12,4
查看答案和解析>>
科目: 来源: 题型:
现要完成下列3项抽样调查:
①从10盒酸奶中抽取3盒进行食品卫生检查.
②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众.报告会结束后,为了听取意见,需要请32名听众进行座谈.
③东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.
较为合理的抽样方法是( )
A.①简单随机抽样,②系统抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①系统抽样,②简单随机抽样,③分层抽样
D.①分层抽样,②系统抽样,③简单随机抽样
查看答案和解析>>
科目: 来源: 题型:
已知A,B分别是椭圆C1:  +
+ =1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2:
=1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2:  -
-  =1上异于A,B的任意一点,a>b>0.
=1上异于A,B的任意一点,a>b>0.
(1)若P(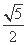 ,
, ),Q(
),Q( ,1),求椭圆C1的方程;
,1),求椭圆C1的方程;
(2)记直线AP,BP,AQ,BQ的斜率分别是k1,k2,k3,k4,求证:k1·k2+k3·k4为定值.
查看答案和解析>>
科目: 来源: 题型:
已知椭圆C1的中心在坐标原点,两个焦点分别为F1(-2,0),F2(2,0),点A(2,3)在椭圆C1上,过点A的直线L与抛物线C2:x2=4y交于B,C两点,抛物线C2在点B,C处的切线分别为l1,l2,且l1与l2交于点P.
(1)求椭圆C1的方程;
(2)是否存在满足|PF1|+|PF2|=|AF1|+|AF2|的点P?若存在,指出这样的点P有几个(不必求出点P的坐标);若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
已知双曲线 -
- =1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为( )
=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为( )
(A)y=±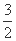 x (B)y=±
x (B)y=±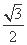 x
x
(C)y=± x (D)y=±
x (D)y=± x
x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com