
科目: 来源: 题型:
定义在R上的可导函数 f(x)=x2 + 2xf′(2)+15,在闭区间[0,m]上有最大值15,最小值-1,
则m的取值范围是( )
A.m≥2 B.2≤m≤4 C.m≥4 D.4≤m≤8
查看答案和解析>>
科目: 来源: 题型:
已知函数y=f(x)的导函数y=f′(x)的图象如图,则( )
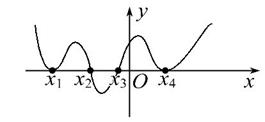 A.函数f(x)有1个极大值点,1个极小值点
A.函数f(x)有1个极大值点,1个极小值点
B.函数f(x)有2个极大值点,2个极小值点
C.函数f(x)有3个极大值点,1个极小值点
D.函数f(x)有1个极大值点,3个极小值点
查看答案和解析>>
科目: 来源: 题型:
用反证法证明命题:“若a,b∈N,ab能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
A.a,b都能被5整除 B.a,b都不能被5整除
C.a,b有一个能被5整除 D.a,b有一个不能被5整除
查看答案和解析>>
科目: 来源: 题型:
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为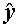 =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心 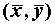
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
查看答案和解析>>
科目: 来源: 题型:
已知椭圆 :
: (
( )的左右两个焦点分别为
)的左右两个焦点分别为 、
、 ,点
,点 在椭圆
在椭圆 上,且
上,且 ,
, ,
, .
.
(1)求椭圆 的标准方程;(7分)
的标准方程;(7分)
(2)若直线 过圆
过圆 的圆心
的圆心 ,交椭圆
,交椭圆 于
于 、
、 两点,且
两点,且 、
、 关于点
关于点 对称,求直线
对称,求直线 的方程.(7分)
的方程.(7分)
查看答案和解析>>
科目: 来源: 题型:
在随机抽查某中学高二级140名学生是否晕机的情况中,已知男学生56人,其中晕机有 人;女学生中不会晕机的为
人;女学生中不会晕机的为 人.不会晕机的男学生中有2人成绩优秀,不会晕机的女生中有4人成绩优秀.
人.不会晕机的男学生中有2人成绩优秀,不会晕机的女生中有4人成绩优秀.
(1)完成下面 列联表的空白处;(5分)
列联表的空白处;(5分)
| 晕机 | 不会晕机 | 合计 | |
| 男学生 | 28 | 56 | |
| 女学生 | 56 | ||
| 合计 | 140 |
(2)能否在犯错误的概率不超过0.05的前提下认为是否晕机与性别有关系?( 保留三位小数)(5分)
保留三位小数)(5分)
(3)若从不会晕机的6名成绩优秀的学生中随机抽取2人去国外参加数学竞赛,试求所抽取的2人中恰有一人是男学生、一人是女学生的概率.(4分)
注:①参考公式: ,其中
,其中 .
.
②常用数据表如下:
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com