
科目: 来源: 题型:
某单位1 000名青年职员的体重x kg服从正态分布N(μ,22),且正态分布的密度曲线如图所示,若体重在58.5~62.5 kg之间属于正常情况,则这1 000名青年职员中体重属于正常情况的人数约是(其中Φ(1)≈0.841)( )
A.682 B.841 C.341 D.667

查看答案和解析>>
科目: 来源: 题型:
设随机变量ξ~B(n,p),且E(ξ)=1.6,D(ξ)=1.28,则( )
A.n=8,p=0.2 B.n=4,p=0.4
C.n=5,p=0.32 D.n=7,p=0.45
查看答案和解析>>
科目: 来源: 题型:
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),P、Q分别为直线l与x轴、y轴的交点,线段PQ的中点为M.
(t为参数),P、Q分别为直线l与x轴、y轴的交点,线段PQ的中点为M.
(1)求直线l的直角坐标方程;
(2)以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
查看答案和解析>>
科目: 来源: 题型:
已知圆C1的参数方程为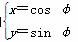 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=2cos
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ=2cos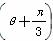 .
.
(1)将圆C1的参数方程化为普通方程,将圆C2的极坐标方程化为直角坐标方程;
(2)圆C1、C2是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
曲线C1的参数方程为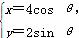 (θ为参数),曲线C2的极坐标方程为ρ=2cos θ-2sin θ.
(θ为参数),曲线C2的极坐标方程为ρ=2cos θ-2sin θ.
(1)化曲线C1,C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)设曲线C1与x轴的一个交点的坐标为P(m,0)(m>0),经过点P作曲线C2的切线l,求切线l的方程.
查看答案和解析>>
科目: 来源: 题型:
在直角坐标系xOy中,圆C1和C2的参数方程分别是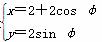 (φ为参数)和
(φ为参数)和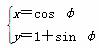 (φ为参数).以O为极点,x轴的正半轴为极轴建立极坐标系.
(φ为参数).以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求圆C1和C2的极坐标方程;
(2)射线OM:θ=α与圆C1的交点为O、P,与圆C2的交点为O、Q,求|OP|·|OQ|的最大值.
查看答案和解析>>
科目: 来源: 题型:
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sin θ,ρcos =2
=2 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
查看答案和解析>>
科目: 来源: 题型:
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.已知点A的极坐标为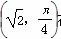 ,直线l的极坐标方程为ρcos
,直线l的极坐标方程为ρcos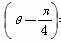 =a,且点A在直线l上.
=a,且点A在直线l上.
(1)求a的值及直线l的直角坐标方程;
(2)圆C的参数方程为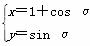 (α为参数),试判断直线l与圆C的位置关系.
(α为参数),试判断直线l与圆C的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com