
科目: 来源: 题型:
对四对变量y和x进行线性相关检验,已知n是观测值组数,r是相关系数,且已知:①n=7,r=0.953 3;②n=15,r=0.301 2;③n=17,r=0.499 1;④n=3,r=0.995 0.则变量y和x具有线性相关关系的是________________.
查看答案和解析>>
科目: 来源: 题型:
为了研究两个变量x和y之间的线性相关性,甲、乙两位同学各自独立地做了10次和15次试验,并且利用线性回归方程,求得回归直线分别为l1和l2.已知两个人在试验中发现对变量x的观测数据的平均值都为s,对变量y的观测数据的平均值都为t,那么下列说法正确的是 ________.
①l1与l2相交,交点为(s,t);
②l1与l2相交,交点不一定是(s,t);
③l1与l2必关于点(s,t)对称;
④l1与l2必定重合.
查看答案和解析>>
科目: 来源: 题型:
某皮肤病医院调查某桑场采桑员和辅助工桑毛虫皮炎发病情况,结果如下表:
|
| 采 桑 | 不采桑 | 总 计 |
| 患者人数 | 18 | 12 | 30 |
| 健康人数 | 6 | 78 | 84 |
| 总计 | 24 | 90 | 114 |
则有________的把握认为发生皮炎与工种有关.
查看答案和解析>>
科目: 来源: 题型:
如图2,一个小球从M处投入,通过管道自上而下落到A或B或C.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A、B、C,则分别设为1,2,3等奖.
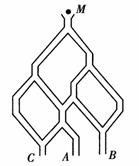
图2
(1)已知获得1,2,3等奖的折扣率分别为50%,70%,90%.记随变量ξ为获得k(k=1,2,3)等奖的折扣率.求随机变量ξ的概率分布及期望E(ξ);
(2)若有3人次(投入1球为1人次)参加促销活动,记随机变量η为获得1等奖或2等奖的人次,求P(η=2).
查看答案和解析>>
科目: 来源: 题型:
某厂生产甲、乙两种产品,生产甲产品一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%.生产1件甲产品,若是一等品可获利4万元,若是二等品则要亏损1万元;生产1件乙产品,若是一等品可获利6万元,若是二等品则亏损2万元.设生产各件产品相互独立.
(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的概率分布;
(2)求生产4件甲产品所获得的利润不少于10万元的概率.
查看答案和解析>>
科目: 来源: 题型:
某校校运会期间,来自甲、乙两个班级共计6名学生志愿者随机平均分配到后勤组、保洁组、检录组,并且后勤组至少有一名甲班志愿者的概率为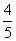 .
.
(1)求6名志愿者中来自甲、乙两个班级的学生各有几人;
(2)设在后勤组的甲班志愿者人数为X,求随机变量X的概率分布及数学期望E(X).
查看答案和解析>>
科目: 来源: 题型:
设离散型随机变量X的概率分布为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0.2 | 0.1 | 0.1 | 0.3 | m |
(1)求2X+1的概率分布;
(2)求|X-1|的概率分布.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com