在直角坐标系xOy中，曲线Cl的参数方程为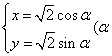为参

    数），以原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为

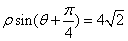
    （I）求曲线Cl的普通方程与曲线C2的直角坐标方程；

    （Ⅱ）设P为曲线C1上的动点，求点P到C2上点的距离的最小值，并求此时点P的直角坐标．

    如图，AB是圆O的直径，C、F为圆O上的点，CA是∠BAF的角平分线．过点C作CD⊥AF交AF的延长线于点D，CM ⊥AB，垂足为点M．

    （I）求证：DC是圆O的切线；

    （Ⅱ）求证：AM·MB =DF·DA．

    已知函数

    （I）若k=e，试确定函数的单调区间；

    （ II）若k>0，且对于任意恒成立，试确定实数k的取值范围，

    已知抛物线C:x2 =2py（p >0）的焦点为F，准线为为抛物线C上一点，已知以F为圆心，FA为半径的圆F交于B、D两点．

    （I）若∠BFD =90°，且△BFD的面积为4，求p的值及圆F的方程；

    （Ⅱ）若A、B、F三点在l司一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m、n距离的比值．

    某学校有A、B、C三个年级，每个年级男女学生人数如下表：

    按年级用分层抽样的方法，在这所学校抽取学生50名，其中有A年级学生10名．

    （I）求z的值；

    （Ⅱ）用分层抽样的方法在C年级中抽取一个容量为5的样本，将该样本看成一个总体，从中任取2名，求至少有1名是男生的概率；

    （Ⅲ）用随机抽样的方法从B年级中抽取8名，经测试他们的体能得分如下：

             9．4    8．6    9．2    9．6    8．7   9．3    9．0   8．2

    把这8名学生的得分看成一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0．5的概率．

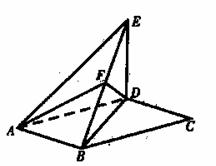
    如图，平行四边形ABCD中，∠DAB=60°，AB=2，AD=4；将

    △CBD沿BD折起到△EBD的位置，使平面EBD⊥平面ABD。

    （1）求证：AB⊥DE；

    （2）若点F为BE的中点，求直线AF与平面ADE所成角正弦值。

    已知△ABC的角A、B、C所对的边分别为a、b、c，设向量P=（a,b），q=（sinB，sinA），n=（b －2，a－2）．

    （I）若P∥q，求证：△ABC等腰三角形；

    （Ⅱ）若P⊥n，边长c=2，∠C=，求△ABC的面积。

已知椭圆的左顶点为A，左焦点为F，点P为该椭圆上任意一点；若该椭圆的上顶点到焦点的距离为2，离心率e=，则·的取值范围是                    .

已知各项均为正数的等比数列{an}的前n项和为Sn，若S4=3S2，a3 =2，

则a7                  .

曲线y=x（21nx +1）在点（1，1）处的切线方程            。