
科目: 来源: 题型:
学习曲线是1936年美国康乃尔大学T.P.Wright博士在飞机制造过程中,通过对大量有关资料、案例的观察、分析、研究,首次发现并提出来的.已知某类学习任务的学习曲线为:f(t)=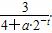 ·100%(其中f(t)为掌握该任务的程度,t为学习时间),且这类学习任务中的某项任务满足f(2)=60%.
·100%(其中f(t)为掌握该任务的程度,t为学习时间),且这类学习任务中的某项任务满足f(2)=60%.
(1)求f(t)的表达式,计算f(0)并说明f(0)的含义;
(2)已知2x>xln2对任意x>0恒成立,现定义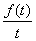 为该类学习任务在t时刻的学习效率指数,研究表明,当学习时间t∈(1,2)时,学习效率最佳,当学习效率最佳时,求学习效率指数相应的取值范围.
为该类学习任务在t时刻的学习效率指数,研究表明,当学习时间t∈(1,2)时,学习效率最佳,当学习效率最佳时,求学习效率指数相应的取值范围.
查看答案和解析>>
科目: 来源: 题型:
一艘渔艇停泊在距岸9km处,今需派人送信给距渔艇3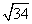 km处的海岸渔站,如果送信人步行速度每小时5km,船行速度每小时4km,问应在何处登岸再步行可以使抵达渔站的时间最省?
km处的海岸渔站,如果送信人步行速度每小时5km,船行速度每小时4km,问应在何处登岸再步行可以使抵达渔站的时间最省?
查看答案和解析>>
科目: 来源: 题型:
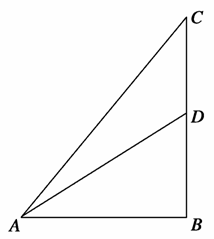
某单位用木料制作如图所示的框架,框架的下部是边长分别为x、y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为8m2,问x、y分别为多少时用料最省?(精确到0.001m) 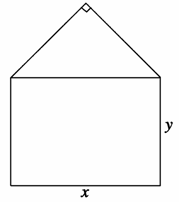
查看答案和解析>>
科目: 来源: 题型:
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
查看答案和解析>>
科目: 来源: 题型:
甲乙两地相距400km,汽车从甲地匀速行驶到乙地,速度不得超过100km/h,已知该汽车每小时的运输成本P(元)关于速度v(km/h)的函数关系是P=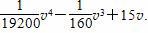 .
.
(1)求全程运输成本Q(元)关于速度v的函数关系式;
(2)为使全程运输成本最少,汽车应以多大速度行驶?并求此时运输成本的最小值.
查看答案和解析>>
科目: 来源: 题型:
已知函数f(x)= +xlnx,g(x)=x3-x2-x-1.
+xlnx,g(x)=x3-x2-x-1.
(1)如果存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M,求满足该不等式的最大整数M;
(2)如果对任意的s,t∈[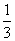 ,2],都有f(s)≥g(t)成立,求实数a的取值范围.
,2],都有f(s)≥g(t)成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
设函数y=x2-2x+2的图象为C1,函数y=-x2+ax+b的图象为C2,已知过C1与C2的一个交点的两切线互相垂直.
(1)求a,b之间的关系;
(2)求ab的最大值.
查看答案和解析>>
科目: 来源: 题型:
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为t元(t为常数,且2≤t≤5),设该食品厂每公斤蘑菇的出厂价为x元(25≤x≤40),根据市场调查,日销售量q与ex成反比,当每公斤蘑菇的出厂价为30元时,销售量为100kg.(每日利润=日销售量×(每公斤出厂价-成本价-加工费)).
(1)求该工厂的每日利润y元与每公斤蘑菇的出厂价x元的函数关系式;
(2)若t=5,当每公斤蘑菇的出厂价x为多少元时,该工厂的利润y最大,并求最大值.
查看答案和解析>>
科目: 来源: 题型:
某工厂生产某种儿童玩具,每件玩具的成本价为30元,并且每件玩具的加工费为t元(其中t为常数,且2≤t≤5),设该工厂每件玩具的出厂价为x元(35≤x≤41),根据市场调查,日销售量与ex(e为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
(1)求该工厂的日利润y(元)与每件玩具的出厂价x元的函数关系式;
(2)当每件玩具的日售价为多少元时,该工厂的利润y最大,并求y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com