
科目: 来源: 题型:
阅读下面的四段话,其中不是解决问题的算法的是( )
A.求1×2×3的值,先计算1×2=2,再计算2×3=6,最终结果为6
B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1
C.今天,我上了8节课,真累
D.求1+2+3+4+5的值,先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为15
查看答案和解析>>
科目: 来源: 题型:
阅读下面的算法:
第一步,输入两个实数a,b.
第二步:若a<b,则交换a,b的值,否则执行第三步.
第三步,输出a.
这个算法输出的是( )
A.a,b中的较大数 B.a,b中的较小数
C.原来的a的值 D.原来的b的值
查看答案和解析>>
科目: 来源: 题型:
下列语句表达中是算法的有( )个( )
①从济南去巴黎可以先乘火车到北京,再乘飞机到巴黎;
②利用公式S=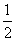 ah计算底为1,高为2的三角形的面积;
ah计算底为1,高为2的三角形的面积;
③解不等式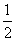 x>2x+4;
x>2x+4;
④求过点M(1,2)与点N(-3,-5)的直线的方程,可先求直线的斜率,再利用点斜式求得方程.
A.1 B.2
C.3 D.4
查看答案和解析>>
科目: 来源: 题型:
以下关于算法的说法正确的是( )
A.描述算法可以有不同的方式,可用形式语言也可用其它语言
B.算法可以看成按照要求设计好的有限的确切的计算序列,并且这样的步骤或序列只能解决当前问题
C.算法过程要一步一步执行,每一步执行的操作必须确切,不能含混不清,而且经过有限步或无限步后能得出结果
D.算法要求按部就班地做,每一步可以有不同的结果
查看答案和解析>>
科目: 来源: 题型:
定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y∈R,有f(x+y)=f(x)·f(y),f(1)=2.
(1)求f(0)的值;
(2)求证:对任意x∈R,都有f(x)>0;
(3)解不等式f(3-2x)>4.
查看答案和解析>>
科目: 来源: 题型:
为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.57元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分按每度0.5元计算.
(1)设月用电x度时,应交电费y元.写出y关于x的函数关系式;
(2)小明家第一季度交纳电费情况如下:
| 月份 | 一月 | 二月 | 三月 | 合计 |
| 交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
则小明家第一季度共用电多少度?
查看答案和解析>>
科目: 来源: 题型:
设f(x)为定义在R上的偶函数,当0≤x≤2时,y=x;当x>2时,y=f(x)的图象是顶点为P(3,4)且过点A(2,2)的抛物线的一部分.

(1)求函数f(x)在(-∞,-2)上的解析式;
(2)在图中的直角坐标系中画出函数f(x)的图象;
(3)写出函数f(x)的值域和单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com