
科目: 来源: 题型:
一个家庭有两个小孩,则所有可能的基本事件有( )
A.(男,女),(男,男),(女,女)
B.(男,女),(女,男)
C.(男,男),(男,女),(女,男),(女,女)
D.(男,男),(女,女)
查看答案和解析>>
科目: 来源: 题型:
下列试验中,是古典概型的为( )
A.种下一粒花生,观察它是否发芽
B.向正方形ABCD内,任意投掷一点P,观察点P是否与正方形的中心O重合
C.从1、2、3、4四个数中,任取两个数,求所取两数之一是2的概率
D.在区间[0,5]内任取一点,求此点小于2的概率
查看答案和解析>>
科目: 来源: 题型:
猎人在相距100 m处射击一野兔,命中的概率为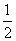 ,如果第一次未击中,则猎人进行第二次射击,但距离已是150 m,如果又未击中,则猎人进行第三次射击,但距离已是200 m,已知此猎人命中的概率与距离的平方成反比,求射击不超过三次击中野兔的概率.
,如果第一次未击中,则猎人进行第二次射击,但距离已是150 m,如果又未击中,则猎人进行第三次射击,但距离已是200 m,已知此猎人命中的概率与距离的平方成反比,求射击不超过三次击中野兔的概率.
查看答案和解析>>
科目: 来源: 题型:
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间 (分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(1)确定x,y的值,并估计顾客一次购物的结算时间的平均值.
(2)求一位顾客一次购物的结算时间不超过2分钟的概率.(将频率视为概率)
查看答案和解析>>
科目: 来源: 题型:
某商场有甲、乙两种电子产品可供顾客选购.记事件A为“只买甲产品”,事件B为“至少买一种产品”,事件C为“至多买一种产品”,事件D为“不买甲产品”,事件E为“一种产品也不买”.判断下列事件是不是互斥事件,如果是,再判断它们是不是对立事件.
(1)A与C;
(2)B与E;
(3)B与D;
(4)B与C;
(5)C与E.
查看答案和解析>>
科目: 来源: 题型:
甲射击一次,中靶概率是P1,乙射击一次,中靶概率是P2,已知 ,
, 是方程x2-5x+6=0的根,且P1满足方程x2-x+
是方程x2-5x+6=0的根,且P1满足方程x2-x+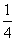 =0.则甲射击一次,不中靶概率为________;乙射击一次,不中靶概率为________.
=0.则甲射击一次,不中靶概率为________;乙射击一次,不中靶概率为________.
查看答案和解析>>
科目: 来源: 题型:
经统计某储蓄所一个窗口等候的人数及相应的概率如下:
| 排队人数 | 0 | 1 | 2 | 3 | 4 | 5人及5人以上 |
| 概率 | t | 0.3 | 0.16 | 0.3 | 0.1 | 0.04 |
(1)t=________;
(2)至少3人排队等候的概率是________.
查看答案和解析>>
科目: 来源: 题型:
围棋盒子中有多粒黑子和白子,已知从中取出2粒都是黑子的概率为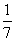 ,从中取出2粒都是白子的概率是
,从中取出2粒都是白子的概率是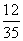 .则从中任意取出2粒恰好是同一色的概率是( )
.则从中任意取出2粒恰好是同一色的概率是( )
A.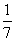 B.
B.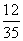
C. D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com