
科目: 来源: 题型:
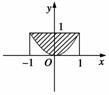
利用计算机随机模拟方法计算图中阴影部分(如图所示).第一步:利用计算机产生两个0~1之间的均匀随机数,x,y,其中-1<x<1,0<y<1;
第二步:拟(x,y)为点的坐标.共做此试验N次.若落在阴影部分的点的个数为N1,
则可以计算阴影部分的面积S.
例如,做了2 000次试验,即N=2 000,
模拟得到N1=1 396,
所以S=________.
查看答案和解析>>
科目: 来源: 题型:
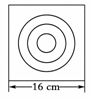 如图所示,在墙上挂着一块边长为16 cm的正方形木块,上面画了小、中、大三个同心圆,半径分别为2 cm,4 cm,6 cm,某人站在3 m之外向此板投镖,设镖击中线上或没有投中木板时不算,可重投,
如图所示,在墙上挂着一块边长为16 cm的正方形木块,上面画了小、中、大三个同心圆,半径分别为2 cm,4 cm,6 cm,某人站在3 m之外向此板投镖,设镖击中线上或没有投中木板时不算,可重投,
记事件A={投中大圆内},
事件B={投中小圆与中圆形成的圆环内},
事件C={投中大圆之外}.
(1)用计算机产生两组[0,1]内的均匀随机数,a1=RAND,b1=RNAD.
(2)经过伸缩和平移变换,a=16a1-8,b=16b1-8,得到两组[-8,8]内的均匀随机数.
(3)统计投在大圆内的次数N1(即满足a2+b2<36的点(a,b)的个数),投中小圆与中圆形成的圆环次数N2(即满足4<a2+b2<16的点(a,b)的个数),投中木板的总次数N(即满足上述-8<a<8,-8<b<8的点(a,b)的个数).
则概率P(A)、P(B)、P(C)的近似值分别是( )
A.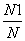 ,
,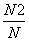 ,
,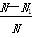 B.
B.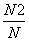 ,
,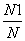 ,
,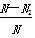
C.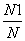 ,
,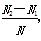 ,
,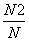 D.
D.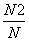 ,
,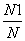 ,
,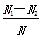
查看答案和解析>>
科目: 来源: 题型:
把[0,1]内的均匀随机数分别转化为[0,4]和[-4,1]内的均匀随机数,需实施的变换分别为( )
A.y=-4x,y=5-4 B.y=4x-4,y=4x+3
C.y=4x,y=5x-4 D.y=4x,y=4x+3
查看答案和解析>>
科目: 来源: 题型:
用均匀随机数进行随机模拟,可以解决( )
A.只能求几何概型的概率,不能解决其他问题
B.不仅能求几何概型的概率,还能计算图形的面积
C.不但能估计几何概型的概率,还能估计图形的面积
D.最适合估计古典概型的概率
查看答案和解析>>
科目: 来源: 题型:
(1)在半径为1的圆的一条直径上任取一点,过该点作垂直于直径的弦,其长度超过该圆内接正三角形的边长 的概率是多少?
的概率是多少?
(2)在半径为1的圆内任取一点,以该点为中点作弦,问其长超过该圆内接正三角形的边长 的概率是多少?
的概率是多少?
(3)在半径为1的圆周上任取两点,连成一条弦,其长超过该圆内接正三角形边长 的概率是多少?
的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
一个路口的红绿灯,红灯亮的时间为30秒,黄灯亮的时间为5秒,绿灯亮的时间为40秒(没有两灯同时亮),当你到达路口时,看见下列三种情况的概率各是多少?
(1)红灯;(2)黄灯;(3)不是红灯.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com