已知{a_n}为等差数列，{b_n}为正项等比数列，公式q≠1，若a₁＝b₁，a₁₁＝b₁₁，则(　　)

A．a₆＝b₆                                                     B．a₆>b₆

C．a₆<b₆                                                       D．以上都有可能

设等差数列{a_n}的前n项和为S_n，若a₂、a₄是方程x²－x－2＝0的两个实数根，则S₅的值为(　　)

A.  B．5  C．－  D．－5

某同学在电脑中打出如下若干个圈：

●○●○○●○○○●○○○○●○○○○○●……

若将此若干个圈依此规律继续下去，得到一系列的圈，那么在前2014个圈中的●的个数是(　　)

A．60  B．61  C．62  D．63

小正方形按照下图中的规律排列：

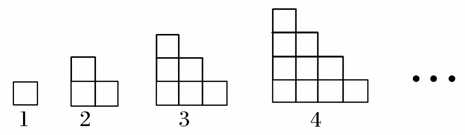
每小图中的小正方形的个数就构成一个数列{a_n}，有以下结论：

①a₅＝15；②数列{a_n}是一个等差数列；③数列{a_n}是一个等比数列；④数列的递推公式为：a_n＝a_n－1＋n(n∈N^*)，其中正确的为(　　)

A．①②④                                                    B．①③④

C．①②                                                        D．①④

已知数列{a_n}，{b_n}满足a₁＝1，且a_n、a_n＋1是函数f(x)＝x²－b_nx＋2ⁿ的两个零点，则b₁₀等于(　　)

A．24　 　 　B．32　 　 　C．48　 　 　D．64

若a、b、c成等比数列，则函数f(x)＝ax²＋bx＋c的图象与x轴交点的个数是(　　)

A．0　　　　B．1　　　　C．2　　　　D．不确定

已知数列{a_n}的前n项和为S_n，且S_n＝4a_n－3(n∈N^*)．

(1)证明：数列{a_n}是等比数列；

(2)若数列{b_n}满足b_n＋1＝a_n＋b_n(n∈N^*)，且b₁＝2，求数列{b_n}的通项公式．

已知数列{a_n}的前n项和为S_n，点(a_n＋2，S_n＋1)在直线y＝4x－5上，其中n∈N^*.令b_n＝a_n＋1－2a_n，且a₁＝1.

(1)求数列{b_n}的通项公式；

(2)若f(x)＝b₁x＋b₂x²＋b₃x³＋…＋b_nxⁿ，求f ′(1)的表达式．

已知数列{a_n}中，a₁＝1，S_n是数列{a_n}的前n项和，且对任意n∈N^*，有a_n＋1＝kS_n＋1(k为常数)．

(1)当k＝2时，求a₂、a₃的值；

(2)试判断数列{a_n}是否为等比数列？请说明理由．

设数列{(－1)ⁿ}的前n项和为S_n，则对任意正整数n，S_n＝(　　)