
科目: 来源: 题型:
四棱锥A-BCDE的正视图和俯视图如下,其中俯视图是直角梯形.
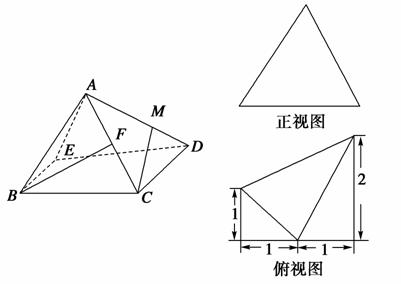
(1)若正视图是等边三角形,F为AC的中点,当点M在棱AD上移动时,是否总有BF丄CM,请说明理由;
(2)若AB=AC,平面ABC与平面ADE所成的锐二面角为45°,求直线AD与平面ABE所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
如图1,在Rt△ABC中,∠C=90°,D、E分别为AC、AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
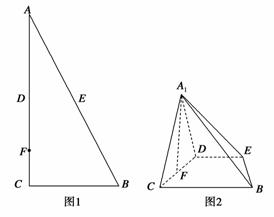
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
查看答案和解析>>
科目: 来源: 题型:
在长方体ABCD-A1B1C1D1中,AA1=AD=2,E是棱CD上的一点.
(1)求证:AD1⊥平面A1B1D;
(2)求证:B1E⊥AD1;
(3)若E是棱CD的中点,在棱AA1上是否存在点P,使得DP∥平面B1AE?若存在,求出线段AP的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图,直四棱柱ABCD-A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD=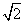 ,AA1=3,E为CD上一点,DE=1,EC=3.
,AA1=3,E为CD上一点,DE=1,EC=3.
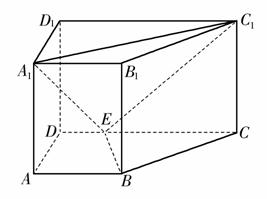
(1)证明:BE⊥平面BB1C1C;
(2)求点B1 到平面EA1C1 的距离.
查看答案和解析>>
科目: 来源: 题型:
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=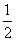 BC.
BC.
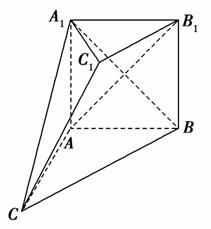
(1)求证:平面A1AC⊥平面ABC;
(2)求证:AB1∥平面A1C1C.
查看答案和解析>>
科目: 来源: 题型:
如图,在几何体ABCDE中,AB=AD=2,AB⊥AD,AE⊥平面ABD.M为线段BD的中点,MC∥AE,AE=MC=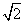 .
.
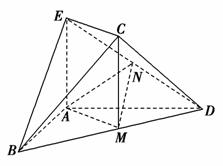
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
查看答案和解析>>
科目: 来源: 题型:
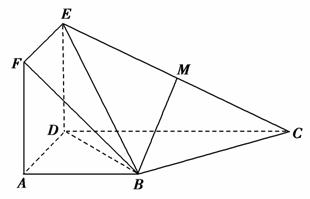
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
(1)求证:BM∥平面ADEF;
(2)求证:平面BDE⊥平面BEC.
查看答案和解析>>
科目: 来源: 题型:
如图,矩形AMND所在的平面与直角梯形MBCN所在的平面互相垂直,MB∥NC,MN⊥MB.
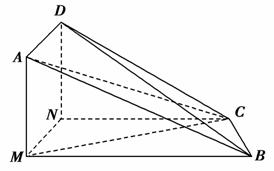
(1)求证:平面AMB∥平面DNC;
(2)若MC⊥CB,求证BC⊥AC.
查看答案和解析>>
科目: 来源: 题型:
已知正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是AB、BC、B1C1的中点.下列命题正确的是________(写出所有正确命题的编号).
①以正方体的顶点为顶点的三棱锥的四个面最多只有三个面是直角三角形;
②P在直线FG上运动时,AP⊥DE;
③Q在直线BC1上运动时,三棱锥A-D1QC的体积不变;
④M是正方体的面A1B1C1D1内到点D和C1距离相等的点,则M点的轨迹是一条线段.
查看答案和解析>>
科目: 来源: 题型:
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足______时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)
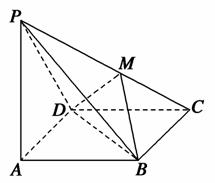
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com