
科目: 来源: 题型:
某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.

(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)

乙的频数统计表(部分)
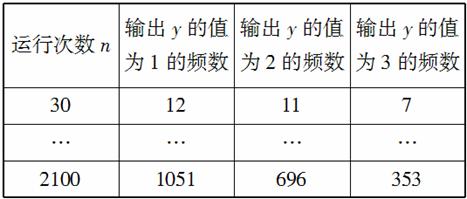
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大;
(3)将按程序框图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
| 降水量X | X<300 | 300≤X<700 | 700≤X<900 | X≥900 |
| 工期延误天数Y | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量X小于300、700、900的概率分别为0.3、0.7、0.9.求:
(1)工期延误天数Y的均值与方差;
(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
查看答案和解析>>
科目: 来源: 题型:
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为ξ.
(1)求ξ的分布列;
(2)求1件产品的平均利润(即ξ的均值);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
查看答案和解析>>
科目: 来源: 题型:
某班将要举行篮球投篮比赛,比赛规则是:每位选手可以选择在A区投篮2次或选择在B区投篮3次.在A区每进一球得2分,不进球得0分;在B区每进一球得3分,不进球得0分,得分高的选手胜出.已知参赛选手甲在A区和B区每次投篮进球的概率分别为 或
或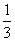 .
.
(1)如果选手甲以在A、B区投篮得分的期望较高者为选择投篮区的标准,问选手甲应该选择在哪个区投篮?
(2)求选手甲在A区投篮得分高于在B区投篮得分的概率.
查看答案和解析>>
科目: 来源: 题型:
甲罐中有5个红球、2个白球和3个黑球,乙罐中有4个红球、4个白球和2个黑球,先从甲罐中任意取出一球放入乙罐,再从乙罐中取出一球,则从乙罐中取出的球是白球的概率为________.
查看答案和解析>>
科目: 来源: 题型:
抛掷一枚均匀的正方体骰子,观察出现的点数,如果出现了5点或6点,则称“抛掷高效”,若“抛掷高效”则得1分,否则得0分,则抛掷一次得分的期望为________.
查看答案和解析>>
科目: 来源: 题型:
两个实习生每人加工一个零件,加工为一等品的概率分别为 和
和 ,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
,两个零件是否加工为一等品相互独立,则这两个零件中恰有一个一等品的概率为( )
A.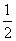 B.
B.
C.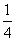 D.
D.
查看答案和解析>>
科目: 来源: 题型:
一台机器生产某种产品,如果生产一件甲等品可获利50元,生产一件乙等品可获利30元,生产一件次品,要赔20元,已知这台机器生产甲等品、乙等品和次品的概率分别为0.6、0.3和0.1,则这台机器每生产一件产品,平均预期可获利( )
A.39元 B.37元
C.20元 D.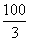 元
元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com