已知f（x）=lnx，g（x）=af（x）+f′（x），

（1）求g（x）的单调区间；

（2）当a=1时，    ①比较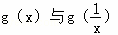的大小；

②是否存在x₀＞0，使得|g（x）﹣g（x₀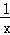）|＜对任意x＞0成立？若存在，求出x₀的取值范围；若不存在，请说明理由．

已知椭圆C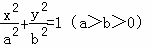：的右焦点为F（1，0），且点（﹣1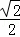，）在椭圆C上．

（1）求椭圆C的标准方程；

（2）已知动直线l过点F，且与椭圆C交于A，B两点，试问x轴上是否存在定点Q，使得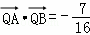恒成立？若存在，求出点Q的坐标，若不存在，请说明理由．

数列{a_n}是递增的等差数列，且a₁+a₆=﹣6，a₃•a₄=8．

（1）求数列{a_n}的通项公式；

（2）求数列{a_n}的前n项和S_n的最小值；

（3）求数列{|a_n|}的前n项和T_n．

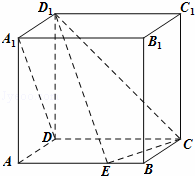
如图，在棱长为1的正方体ABCD﹣A₁B₁C₁D₁中，点E是棱AB上的动点．

（Ⅰ）求证：DA₁⊥ED₁；

（Ⅱ）若直线DA₁与平面CED₁成角为45°，求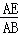的值；

（Ⅲ）写出点E到直线D₁C距离的最大值及此时点E的位置（结论不要求证明）．

在△ABC中，BC=a，AC=b，a、b是方程的两个根，且A+B=120°，求△ABC的面积及AB的长．

袋中装有黑球和白球共7个，从中任取2个球都是黑球的概率为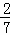，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取…，取球后不放回，直到两人中有一人取到白球时终止，每个球在每一次被取出的机会是等可能的，用ξ表示取球终止所需要的取球次数．

（Ⅰ）求随机变量ξ的分布列及数学期望；

（Ⅱ）求乙取到白球的概率．

等腰Rt△ACB，AB=2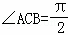，．以直线AC为轴旋转一周得到一个圆锥，D为圆锥底面一点，BD⊥CD，CH⊥AD于点H，M为AB中点，则当三棱锥C﹣HAM的体积最大时，CD的长为_____________.

已知圆的方程为x²+y²﹣6x﹣8y=0，设该圆过点（3，5）的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为______________.

棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如

图所示，那么该几何体的体积是（　　）

记等差数列{a_n}的前n项和为S_n，已知a₂+a₄=6，S₄=10．则a₁₀=　　．