
科目: 来源: 题型:
已知不等式ax2-bx-1≥0的解是[-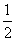 ,-
,-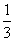 ],则不等式x2-bx-a<0的解是( )
],则不等式x2-bx-a<0的解是( )
A.(2,3) B.(-∞,2)∪(3,+∞)
C.(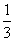 ,
,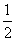 ) D.(-∞,
) D.(-∞,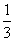 )∪(
)∪(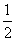 ,+∞)
,+∞)
查看答案和解析>>
科目: 来源: 题型:
甲、乙两大超市同时开业,第一年的全年销售额为a万元,由于经营方式不同,甲超市前n年的总销售额为 (n2-n+2)万元,乙超市第n年的销售额比前一年销售额多a
(n2-n+2)万元,乙超市第n年的销售额比前一年销售额多a n-1万元.
n-1万元.
(1)求甲、乙两超市第n年销售额的表达式;
(2)若其中某一超市的年销售额不足另一超市的年销售额的50%,则该超市将被另一超市收购,判断哪一超市有可能被收购?如果有这种情况,将会出现在第几年?
查看答案和解析>>
科目: 来源: 题型:
设等差数列{an}的前n项和为Sn,公比是正数的等比数列{bn}的前n项和为Tn,已知a1=1,b1=3,a2+b2=8,T3-S3=15.
(1)求{an},{bn}的通项公式;
(2)若数列{cn}满足a1cn+a2cn-1+…+an-1c2+anc1=2n+1-n-2对任意n∈N*都成立,求证:数列{cn}是等比数列.
查看答案和解析>>
科目: 来源: 题型:
设数列{an}的前n项和为Sn,a1=1,Sn=nan-2n(n-1).
(1)求数列{an}的通项公式an;
(2)设数列{ }的前n项和为Tn,求证:
}的前n项和为Tn,求证: ≤Tn<
≤Tn< .
.
查看答案和解析>>
科目: 来源: 题型:
已知点(1,2)是函数f(x)=ax(a>0且a≠1)的图象上一点,数列{an}的前n项和Sn=f(n)-1.
(1)求数列{an}的通项公式;
(2)若bn=logaan+1,求数列{anbn}的前n项和Tn.
查看答案和解析>>
科目: 来源: 题型:
数列{an}中,a1=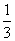 ,前n项和Sn满足Sn+1-Sn=(
,前n项和Sn满足Sn+1-Sn=(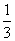 )n+1(n∈N*).
)n+1(n∈N*).
(1)求数列{an}的通项公式an以及前n项和Sn;
(2)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com