
科目: 来源: 题型:
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=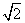 ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.
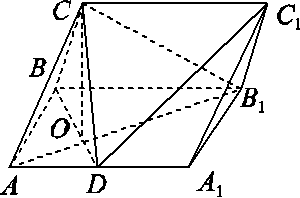
(1)证明:BC⊥AB1;
(2)若OC=OA,求三棱锥C1-ABC的体积.
查看答案和解析>>
科目: 来源: 题型:
下列命题中正确的是________.(填上你认为正确的所有命题的序号)
①空间中三个平面α,β,γ,若α⊥β,γ⊥β,则α∥γ;
②若a,b,c为三条两两异面的直线,则存在无数条直线与a,b,c都相交;
③球O与棱长为a的正四面体各面都相切,则该球的表面积为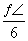 a2;
a2;
④三棱锥P-ABC中,PA⊥BC,PB⊥AC,则PC⊥AB.
查看答案和解析>>
科目: 来源: 题型:
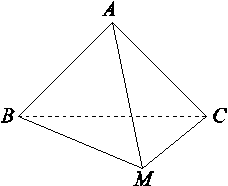
在△ABC中,∠C=90°,∠B=30°,AC=1,M为AB的中点,将△ACM沿CM折起,使A,B间的距离为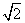 ,如图所示,则M到平面ABC的距离为( )
,如图所示,则M到平面ABC的距离为( )
A.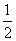 B.
B.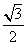 C.1 D.
C.1 D.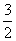
查看答案和解析>>
科目: 来源: 题型:
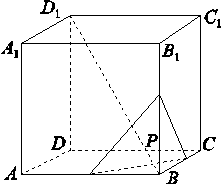
如图,正方体ABCD-A1B1C1D1的棱长为2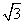 ,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,则当x∈[1,5]时,函数y=f(x)的值域为( )
,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记这样得到的截面多边形(含三角形)的周长为y,设BP=x,则当x∈[1,5]时,函数y=f(x)的值域为( )
A.[2 ,6
,6 ] B.[2
] B.[2 ,18]
,18]
C.[3 ,18] D.[3
,18] D.[3 ,6
,6 ]
]
查看答案和解析>>
科目: 来源: 题型:
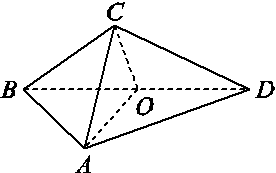
在三棱锥C-ABD中(如图),△ABD与△CBD是全等的等腰直角三角形,O为斜边BD的中点,AB=4,二面角A-BD-C的大小为60°,并给出下面结论:①AC⊥BD;②AD⊥CO;③△AOC为正三角形;④cos ∠ADC=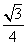 ;⑤四面体ABCD的外接球的表面积为32π.
;⑤四面体ABCD的外接球的表面积为32π.
其中真命题是( )
A.②③④ B.①③④
C.①④⑤ D.①③⑤
查看答案和解析>>
科目: 来源: 题型:
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P长度的取值范围是( )
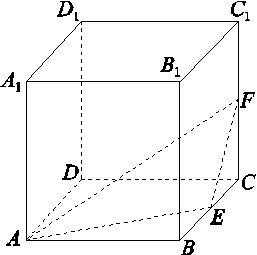
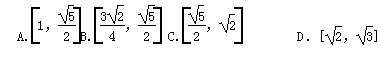
查看答案和解析>>
科目: 来源: 题型:
如图所示,正方体ABCD-A1B1C1D1的棱长为1,BD∩AC=O,M是线段D1O上的动点,过点M作平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为( )

A.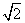 B.
B.
C. D.1
D.1
查看答案和解析>>
科目: 来源: 题型:
已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题:
①若α⊥β,m∥α,则m⊥β;
②若m⊥α,n⊥β,且m⊥n,则α⊥β;
③若m⊥β,m∥α,则α⊥β;
④若m∥α,n∥β,且m∥n,则α∥β.
其中正确命题的序号是( )
A.①④ B.②③
C.②④ D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com