
科目: 来源: 题型:
已知直角坐标系内的两个向量a=(1,3),b=(m,2m-3)使平面内的任意一个向量c都可以唯一地表示成c=λa+μb,则m的取值范围是( )
A.(-∞,0)∪(0,+∞) B.(-∞,-3)∪(-3,+∞)
C.(-∞,3)∪(3,+∞) D.[-3,3)
查看答案和解析>>
科目: 来源: 题型:
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= AD=1,CD=
AD=1,CD=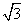 .
.
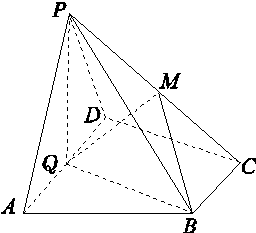
(1)求证:平面PQB⊥平面PAD;
(2)若M为棱PC的中点,求异面直线AP与BM所成角的余弦值;
(3)若二面角M-BQ-C的大小为30°,求QM的长.
查看答案和解析>>
科目: 来源: 题型:
如图,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4,点E,F分别是AB,CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.
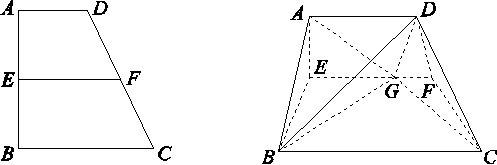
(1)当AG+GC最小时,求证:BD⊥CG;
(2)当2VB-ADGE=VD-GBCF时,求二面角D-BG-C的余弦值.
查看答案和解析>>
科目: 来源: 题型:
如图,在几何体ABCDE中,AB=AD=BC=DC=2,AE=2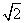 ,AB⊥AD,且AE⊥平面ABD,平面CBD⊥平面ABD.
,AB⊥AD,且AE⊥平面ABD,平面CBD⊥平面ABD.
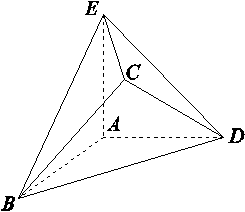
(1)求证:AB∥平面CDE;
(2)求二面角A-EC-D的余弦值.
查看答案和解析>>
科目: 来源: 题型:
P为正方体ABCD-A1B1C1D1对角线BD1上的一点,且BP=λBD1(λ∈(0,1)).下面结论:
①A1D⊥C1P;
②若BD1⊥平面PAC,则λ=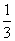 ;
;
③若△PAC为钝角三角形,则λ∈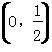 ;
;
④若λ∈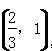 ,则△PAC为锐角三角形.
,则△PAC为锐角三角形.
其中正确的结论为________.(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com