
科目: 来源: 题型:
已知函数f(x)=x2+ ax - lnx,a∈R.
(I)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(II)令g(x)=f(x)-x2,是否存在实数a,当x∈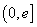 (e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
(e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
已知公差不为零的等差数列{an},满足 al+a3+a5 =12,且a1,a5,a17成等比数列.
(I)求数列{an}的通项公式;
(II)若bn=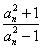 , 数列{bn}的前n项和为Sn,求证:Sn-n<
, 数列{bn}的前n项和为Sn,求证:Sn-n<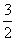 .
.
查看答案和解析>>
科目: 来源: 题型:
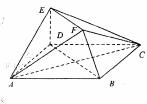
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED =l,EF∥BD,且EF =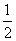 BD.
BD.
(I)求证:BF∥平面ACE;
(II)求证:平面EAC⊥平面BDEF;
(III)求几何体ABCDEF的体积。
查看答案和解析>>
科目: 来源: 题型:
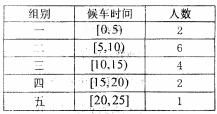
为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候午时间(单位:分钟)作为样本分成5组,如下表所示:
(I)求这15名乘客的平均候车时间;
(II)估讦这60名乘客中候车时间少于10分钟的人数:
(III)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率。
查看答案和解析>>
科目: 来源: 题型:
已知函数,f(x)=Asin(cox+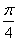 )(其中x∈R,A>0,
)(其中x∈R,A>0,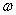 >0)的最大值为2,最小正周期为8.
>0)的最大值为2,最小正周期为8.
(I)求函数f(x)的解析式及单调递增区间:
(II)若函数f(x)图象上的两点P,Q的横坐标依次为2.4,O为坐标原点,求△POQ的面积。
查看答案和解析>>
科目: 来源: 题型:
对于函数f(x),若存在常数a≠0,使得取x定义域内的每一个值,都有f(x)=-f(2a-x),则称f(x)为准奇函数.给出下列函数①f(x)=(x-1)2,②f(x)=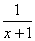 ,③ f(x)=x3,
,③ f(x)=x3,
④f(x)=cosx,其中所有准奇函数的序号是 。
查看答案和解析>>
科目: 来源: 题型:
为了均衡教育资源,加大对偏远地区的教育投入,调查了某地若干户家庭的年收入x(单位:万元)和年教育支出y(单位:万元),调查显示年收入x与年教育支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: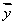 =0.15x+0.2。由回归直线方程可知,家庭年收入每增加1万元,,年教育支出平均增加 万元.
=0.15x+0.2。由回归直线方程可知,家庭年收入每增加1万元,,年教育支出平均增加 万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com