
科目: 来源: 题型:
有5 盆不同菊花, 其中黄菊花2 盆、 白菊花2 盆、 红 菊花1 盆,现把它们摆放成一排, 要求2 盆黄菊花必 须相邻,2 盆白菊花不能相邻, 则这5 盆花不同的摆 放种数是
A.12 B.24
C.36 D.48
查看答案和解析>>
科目: 来源: 题型:
函数 f( x) = s i n(ω x + φ )( x ∈R )( ω> 0 , | φ | <  )的部分图象如图所示, 如果x1 、 x2 ∈
)的部分图象如图所示, 如果x1 、 x2 ∈ ,且f(x1) =f(x2) , 则f(x1 + x2) 等于
,且f(x1) =f(x2) , 则f(x1 + x2) 等于
A.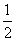 B.
B. C.
C.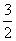 D.1
D.1

查看答案和解析>>
科目: 来源: 题型:
已知a > b > 0 ,椭圆 C1 的方程为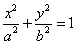 ,双曲线 C2 的方程为
,双曲线 C2 的方程为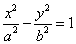 ,C1 与 C2 的离心率之积为
,C1 与 C2 的离心率之积为 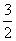 , 则 C1 、 C2 的离心率分别为
, 则 C1 、 C2 的离心率分别为
A.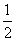 ,3 B.
,3 B.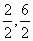 C.
C.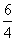 ,2 D.
,2 D.
查看答案和解析>>
科目: 来源: 题型:
下列有关命题的说法正确的是
A.命题“ x ∈R,均有x2- x + 1 > 0”的否定是:“x0 ∈R, 使得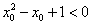 ”;
”;
B.在 △ABC 中,“ s i nA > s i nB”是“A > B”成立的充要条件;
C.线性回归方程y = 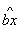 + a 对应的直线一定经过其样本数据点( x 1 , y1)、( x2 , y2)、…,
+ a 对应的直线一定经过其样本数据点( x 1 , y1)、( x2 , y2)、…,
(x n, y n) 中的一个;
D.在2 ×2 列联表中,ad - b c 的值越接近0 ,说明两个分类变量有关的可能性就越大.
查看答案和解析>>
科目: 来源: 题型:
设全集U = R,集合 M= {x | y = lg( x2- 1) } , N= { x|0 < x < 2} ,则 N ∩( 瓓UM ) =
A.{ x | - 2 ≤x < 1} B.{ x | 0 < x ≤1}
C.{ x | - 1 ≤x ≤1} D.{ x | x < 1}
查看答案和解析>>
科目: 来源: 题型:
已知椭圆 的中心在原点
的中心在原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为 .
.
 (1)求椭圆
(1)求椭圆 的方程;
的方程;
(2)如图,动直线 与椭圆
与椭圆 有且仅有一个公共点,点
有且仅有一个公共点,点 是直线
是直线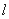 上的两点,
上的两点, 是椭圆的左右焦点,且
是椭圆的左右焦点,且 ,求四边形
,求四边形 面积
面积 的最大值。
的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com